大学物理

资料总结整理人：19级通信工程于邦震

作图：于邦震

电

1. 库仑定律 F

$$
F=k\frac{q_1q_2}{r^2}e_r \ \ \ 又有k=\frac{1}{4\pi\varepsilon _0}
$$

推导出来有
$$
F=\frac{1}{4\pi\varepsilon _0}\frac{q_1q_2}{r^2}\overrightarrow{e_r}= Eq
$$

2. 电场

电场强度 E

$$
E=\frac{\overrightarrow{F}}{q_0}=\frac{1}{4\pi\varepsilon _0}\frac{q}{r^2}\overrightarrow{e_r}
$$

微分形式：
$$
E=\int dE=\frac{1}{4\pi\varepsilon _0}\int_v \frac{dq}{r^2}\overrightarrow{e_r}
$$

$$
dq=
\left{\begin{matrix}
\lambda dL\ \sigma dS\ \rho dV
\end{matrix}\right.
$$

2.2. 电偶极子 $p_e$

$$
p_e=ql
$$

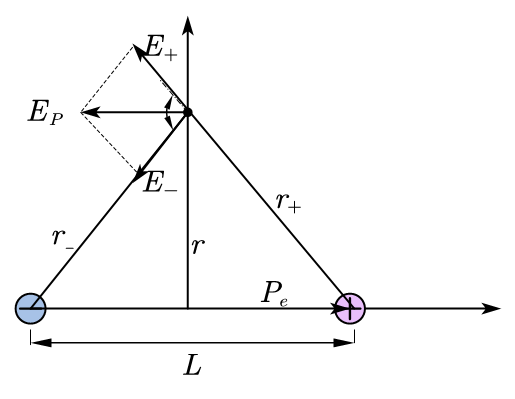
$$
E=-\frac{p_e}{4\pi\varepsilon_0 r^3}
$$

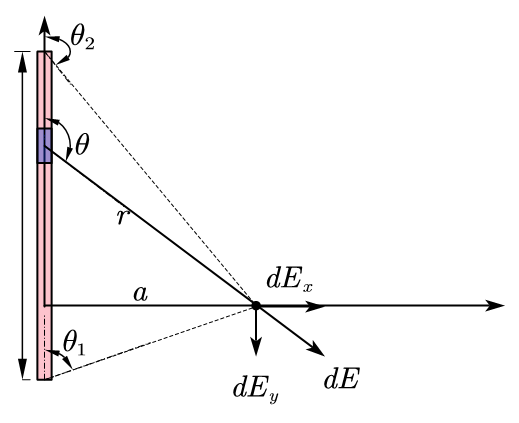
$$
E=
\left{\begin{matrix}
E_x= \frac{\lambda}{2\pi\varepsilon_0 a}\
E_y=0
\end{matrix}\right.
$$

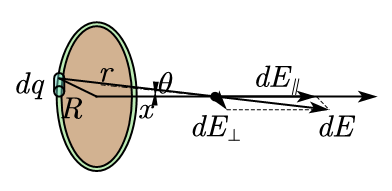
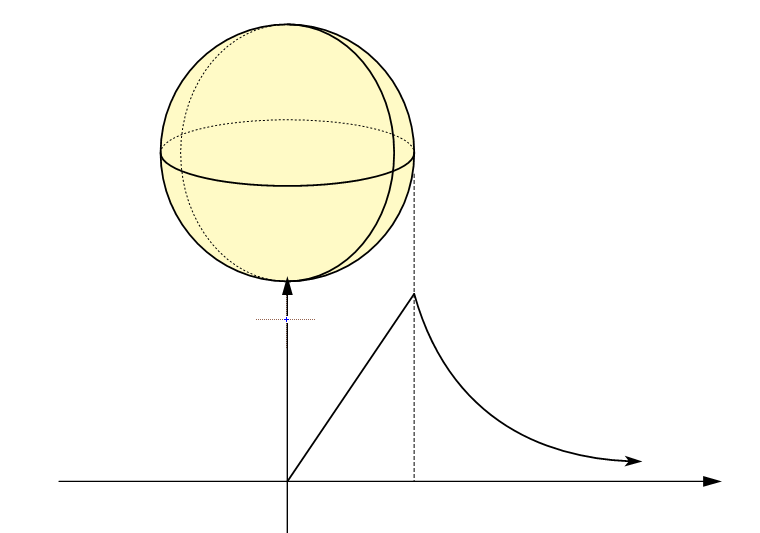
$$
E=E_{\}=\frac{qx}{4\pi\varepsilon_0 \sqrt{(x^2+R^2)^3}}=
\left{\begin{matrix}
x>>R,E=\frac{q}{4\pi\varepsilon_0 x^2};\
x=0,则E=0;\ \ \ \ \ \ \ \ \
由\frac{dE}{dx}=0,知x=\pm \frac{\sqrt{2}}{2}R
\end{matrix}\right.
$$

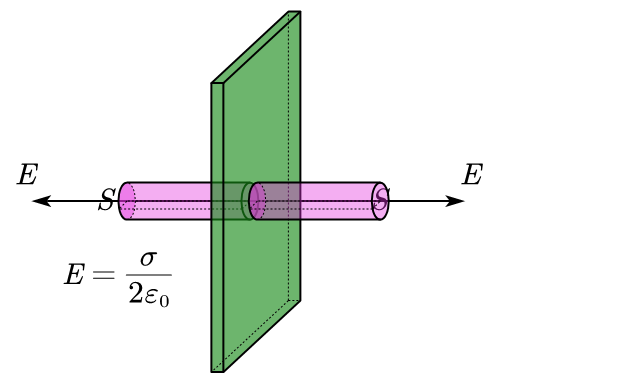
3. 电通量

$$
d\Phi_e=EdS_\perp=EdScos\theta
$$

所以
$$
\Phi_e=\int _sEdS_\perp=\int_s EdScos\theta
$$

4. 静电场的高斯定理$\Phi_e=\oint _sEdS=\frac{1}{\varepsilon _0}\sum_i q_i$

$$
\Phi_e=\oint _sEdS=\frac{1}{\varepsilon _0}\sum_i q_i
$$

5. 静电力做功 W

$$
W=Eqcos\theta l
$$

微分形式
$$
dW=Eqcos\theta dl
$$
所以积分后(这里的E是有方向的)
$$
W_{ab}=W_a-W_b
=\int_a^b q_0Edl
=\frac{q_0q_i}{4\pi\varepsilon_0}\int_{r_a}^{r_b}\frac{1}{r^2}dr
=\frac{q_0q_i}{4\pi\varepsilon_0}(\frac{1}{r_a}-\frac{1}{r_b})
$$

6. 静电场环路定理$\oint_L Edl=0$

$$
\oint_LEqdl=0，则可以写为\oint_L Edl=0.表达是转一圈做功为0
$$

7. 电势

7.1.电势能 W

点电荷q的电势=点电荷q从该点移动到电势为0的点所做的功。
$$
W_p=\int_p^\infty q_0E\cdot dl
$$

7.2.电势与电势差 V

$$
U_p=\frac{W_p}{q_0}=\int_p^\infty E\cdot dl
$$

电势差
$$
U_{ab}=U_a-U_b
=\int_a^\infty E\cdot dl-\int_b^\infty E\cdot dl
=\int_a^b E\cdot dl
$$

8. 点电荷的库仑力、电场、电势

8.1.库仑力

$$
F=\frac{1}{4\pi\varepsilon _0}\frac{q_1q_2}{r^2}\overrightarrow{e_r}
$$

8.2.电场

$$
E=\frac{1}{4\pi\varepsilon _0}\frac{q_0}{r^2}\overrightarrow{e_r}
$$

8.3.电势

$$
U=\frac{1}{4\pi\varepsilon _0}\frac{q}{r^r}
$$

9. 等势面

• 等势面与电场线处处正交垂直

• 电势面密集，场强越大

• 电场线指向电势减弱的方向

9.1. 电场强度与电势梯度

$$
E_l=-\frac{dU}{dl}
$$

电场指向电势降低的方向

• 电势梯度：电势减少的方向

$$
E=-\frac{dU}{dn}\overrightarrow{e_n}=-\bigtriangledown U =-grad U
$$

场强与电势梯度相反

10. 电容

$$
C=\frac{q}{U}
$$

• 求电容的方法

1. 先设电荷
2. 求E(高斯去求)
3. 求$U=\int_A^B E\cdot dl=\frac{qd}{\varepsilon_0S}$
4. 求$C=\frac{q}{U}=\frac{\varepsilon_0S}{qd}$

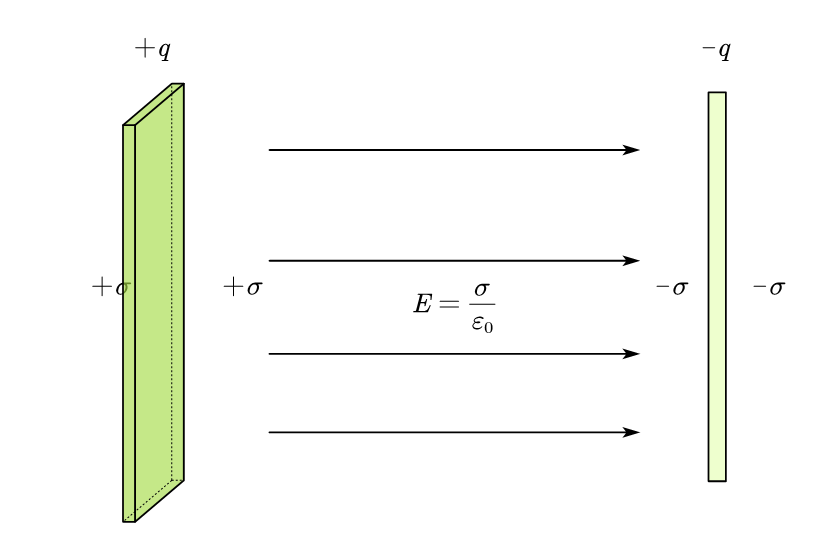
1、平行板电容
$$
\because E=\frac{\sigma}{\varepsilon_0}=\frac{q}{\varepsilon_0S};U_{AB}=\int_A^BE \cdot dl=Ed=\frac{qd}{\varepsilon_0S}
$$

$$
\therefore C=\frac{q}{U_{AB}}=\frac{\varepsilon_0S}{d}
$$

2、圆柱形电容器
$$
\because \lambda=\frac{q}{l}
$$

$$
\therefore E=\frac{\lambda}{2\pi\varepsilon_0r},R_A<r<R_B
$$

$$
\therefore U_{AB}=\int_{R_A}^{R_B}E \cdot dr =\int_{R_A}^{R_B}\frac{\lambda}{2\pi\varepsilon_0r}dr=\frac{\lambda}{2\pi\varepsilon_0}ln\frac{R_B}{R_A}
$$

$$
\therefore C=\frac{q}{U_{AB}}=\frac{\lambda l}{U_{AB}}=\frac{2\pi\varepsilon_0l}{ln\frac{R_B}{R_A}}
$$

3、球型电容器
$$
设(内R_A)(外R_B)球壳分别带电：+q、-q
$$

$$
E=\frac{q}{4\pi\varepsilon_0r^2},(R_A<r<R_B)
$$

$$
U_{AB}=\int_{R_A}^{R_B}E \cdot dr =\frac{q}{4\pi\varepsilon_0}\int_{R_A}^{R_B}\frac{dr}{r^2}=\frac{q}{4\pi\varepsilon_0}(\frac{1}{R_A}-\frac{1}{R_B})
$$

所以电容为
$$
C=\frac{q}{U_{AB}}=\frac{4\pi\varepsilon_0R_AR_B}{R_B-R_A}
$$
当$d=R_B-R_A$很小的时候，$R_BR_A\approx R_A^2$ ,而$4\pi\varepsilon_0R_A^2=S$
$$
有:C=\frac{4\pi\varepsilon_0R_A^2}{d}=\frac{\varepsilon_0S}{d}
$$

10.1. 有电解质的情况

$$
C=\frac{\varepsilon_0\varepsilon_rS}{d}
$$

有电解质后整个电容的静电场
$$
E=E_0-E’=\frac{1}{\varepsilon_0}(\sigma_0-\sigma’)
$$

$$
U_0=\varepsilon_r(Ed)=E_0d
$$

$$
E=\frac{E_0}{\varepsilon_r}
$$

充满介质的电容总电场为真空电容场强的$\frac{1}{\varepsilon_r}$倍

10.2. 高斯定理

$$
\oint_S \varepsilon_r\varepsilon_0E\cdot dS=\sum_iq_i
$$

$$
电位移矢量 ：D=\varepsilon_r\varepsilon_0E=\varepsilon E
$$

$$
\because \oint_S \varepsilon E\cdot dS=\oint_S D\cdot dS=\sigma_0 S=\sum_iq_i
$$

推导：
$$
\oint_S E_{空}\cdot ds=\frac{1}{\varepsilon _0}\sum_i q_i
$$

$$
\oint_S \varepsilon_r \frac{E_{空}}{\varepsilon_r}\cdot ds=\frac{1}{\varepsilon _0}\sum_i q_i
$$

$$
\oint_S \varepsilon_r\varepsilon_0 \frac{E_{空}}{\varepsilon_r}\cdot ds=\sum_i q_i
$$

$$
\oint_S \varepsilon_r\varepsilon_0 E_{介}\cdot ds=\sum_i q_i
$$

$$
\oint_S D\cdot dS=\sigma_0 S=\sum_iq_i
$$

10.3. 静电场的储存能量

$$
C=\frac{q}{U}
$$

$$
dW=Udq=\frac{q}{C}dq
$$

所以有
$$
W=\frac{1}{C}\int_0^Qqdq=\frac{Q^2}{2C}
$$
又因为
$$
Q=CU
$$

所以有
$$
W=\frac{Q^2}{2C}=\frac{1}{2}QU=\frac{CU^2}{2}
$$

10.4. 静电场的能量

$$
E=\frac{\sigma}{\varepsilon}=\frac{Q}{\varepsilon S}
$$

又有
$$
C=\frac{\varepsilon S}{d}
$$
所以有
$$
W_e=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}\frac{\varepsilon^2 S^2E^2d}{\varepsilon S}=\frac{1}{2}\varepsilon SE^2d=\frac{1}{2}\varepsilon E^2V
$$
引入能量密度：
$$
w_e=\frac{W_e}{V}=\frac{1}{2}\varepsilon E^2
$$
所以微分形式：
$$
dW_e=w_edV
$$
所以有：
$$
W_e=\int_VdW_e=\int_Vw_edV=\int_V\frac{1}{2}\varepsilon E^2dV
$$

磁学

（左力右电）

1. 恒定电流

$$
I=\frac{dq}{dt}=I(t)
$$

q为单位载流子电量、n为载流子的数量、u为飘移速度
$$
dI=qnudS_\perp=qnudScos\theta
$$
所以设 电流密度矢量$\delta =qnu$

所以有：
$$
I=\int_S\delta \cdot ds
$$
则
$$
I=\oint_S\delta \cdot ds=0
$$

2. 电源电动势

$$
E为电源电动势(其实就是V):\ \ \ E=\frac{W}{q}
$$

3. 磁场强度

$$
F_{max}=q_0vB;所以B=\frac{F_{max}}{q_0v}
$$

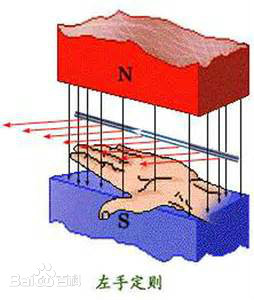
4. 毕奥-萨法尔定律

$$
dB=k\frac{Idlsin\theta}{r^2}=\frac{\mu_0}{4\pi}\frac{Idlsin\theta}{r^2}
$$

$$
dB=k\frac{Idl\times r }{r^3}=\frac{\mu_0}{4\pi}\frac{Idl\times e_r}{r^2}
$$

$$
B=\int dB=\frac{\mu_0}{4\pi}\int\frac{Idl\times e_r}{r^2}
$$

4.1. 长直导线

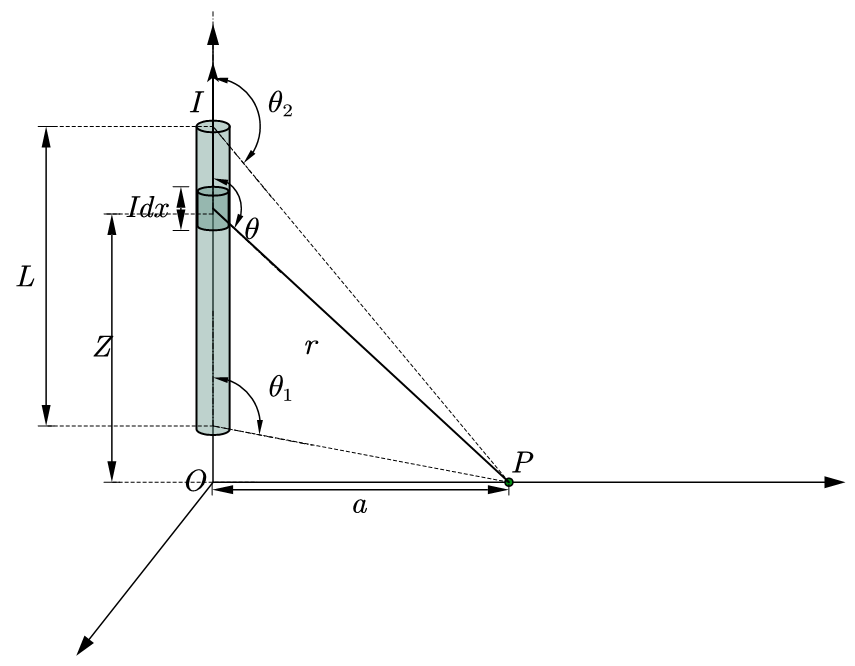
$$
dB=\frac{\mu_0}{4\pi}\frac{Idzsin\theta}{r^2}
$$

$$
z=a\ cot(\pi-\theta)=-a\ cot\theta
$$

$$
dz=d(-acot\theta)=-a\ dcot\theta=acsc^2\theta d\theta
$$

r和$\theta$ 的关系
$$
r=\frac{a}{sin\theta}
$$
带入，得：
$$
B=\int\frac{\mu_0}{4\pi}\frac{Iacsc^2\theta sin^3\theta}{a^2}d\theta=\frac{\mu_0I}{4a\pi}\int_{\theta_1}^{\theta_2}sin\theta d\theta=\frac{\mu_0I}{4a\pi}(cos\theta_1-cos\theta_2)
$$
当为无线长的时候：$\theta_1=0;\theta_2=\pi$:
$$
B=\frac{\mu_0I}{2a\pi}
$$
当为半无线长，$\theta_1=0\ or\ \frac{\pi}{2};\theta_2=\frac{\pi}{2}\ or\ \pi$:
$$
B=\frac{\mu_0I}{4a\pi}
$$

4.2. 圆环轴线附近的磁场

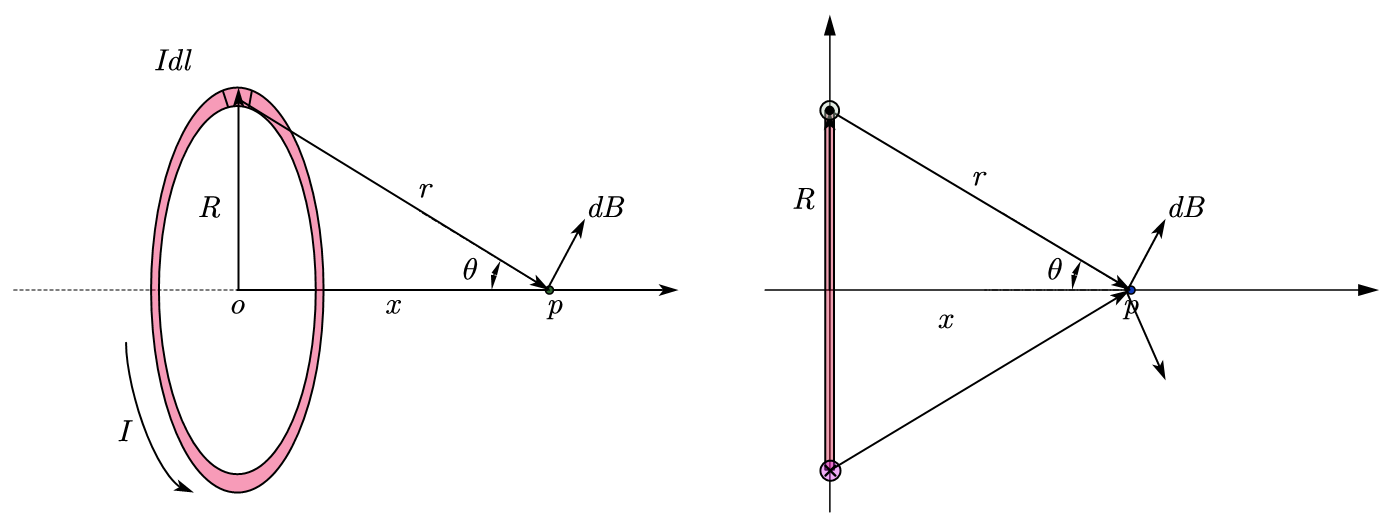
$$
dB=\frac{\mu_0}{4\pi}\frac{Idlsin(90^{\circ})}{r^2}
$$

$$
B_\perp=0
$$

$$
sin\theta=\frac{R}{r}
$$

$$
r=\sqrt{x^2+R^2}
$$

$$
B_{//}=\int dB_{//}=\int dBsin\theta=dB\
=\int_0^{2\pi R}\frac{\mu_0}{4\pi}\frac{Idl}{r^2}\frac{R}{r}\
=\frac{\mu_0IR^2}{2\pi(x^2+R^2)^{\frac{3}{2}}}\
=\frac{\mu_0S}{2\pi(x^2+R^2)^{\frac{3}{2}}}
$$

• 当x=0时：
  $$
  B_0=\frac{\mu_0I}{2R}
  $$

• 当x>>R时：R=0

$$
B
=\frac{\mu_0IR^2}{2 x^3}\
=\frac{\mu_0S}{2\pi x^3}
$$

这里引入载流线圈的磁矩$P_m$有：
$$
P_m=ISe_n\ \ \ \ \ \ or\ \ \ \ \ P_m=NISe_n
$$

4.3. 载流密绕直螺线管内部磁场

推导：

设半径为$R$，通电流$I$,单位长度绕有n匝线圈，求o电处的磁感应强度
$$
由上个知识的公式得知：dB=\frac{\mu_0}{2}\frac{nIR^2dx}{(x^2+R^2)^{\frac{3}{2}}}
$$
因为上下的原因，导致所有的磁感应强度方向相同都向右，整个磁感应强度为B
$$
B=\int dB=\int_{x_1}^{x_2}\frac{\mu_0}{2}\frac{nIR^2dx}{(x^2+R^2)^{\frac{3}{2}}}
$$
所以得：
$$
B=\frac{1}{2}\mu_0nI(cos\beta_2 -cos\beta_1)
$$
当为无线长直螺线管有：
$$
\beta_1=0,\beta_2=\pi;所以：B=\mu_0nI
$$
当为半无线直导线的有段或左端有：
$$
B=\frac{1}{2}\mu_0nI
$$

5. 运动电荷产生的磁场

由
$$
dB=\frac{\mu_0}{4\pi}\frac{Idlsin\theta}{r^2}\ \ \ \ \ 和 \ \ \ \ \ I=nqvS
$$
所以可以得到：
$$
dB=\frac{\mu_0}{4\pi}\frac{nqvSdlsin\theta}{r^2}
$$

$$
dN=nSdl
$$

又有如下的公式：
$$
B=\frac{dB}{dN}=\frac{\mu_0}{4\pi}\frac{qvsin\theta}{r^2}=\frac{\mu_0}{4\pi}\frac{qV\times r}{r^3}
$$
所以：
$$
B=\frac{\mu_0}{4\pi}\frac{qV\times r}{r^3}
$$

6. 真空磁场的高斯定理

6.1. 磁通量 $\Phi_m$

$$
B=\frac{d\Phi_m}{dS_\perp}
$$

$$
d\Phi_m=B\cdot dS
$$

6.2. 高斯定理

$$
\oint _sBdS=0
$$

7. 真空恒定磁场安培环路定理

沿任何路径L一周的B矢量线积分=闭合路径内包含并穿过的电流代数和的$\mu_0$倍，与路径形状无关。
$$
\oint B\cdot dl=\mu_0\sum_iI_i
$$
方向的确定：
$$
对于包围的电流I，当电流与积分路径绕行方向成右手螺旋关系时，电流为正，反之为负。
$$

7.1 无线长圆柱导体磁场

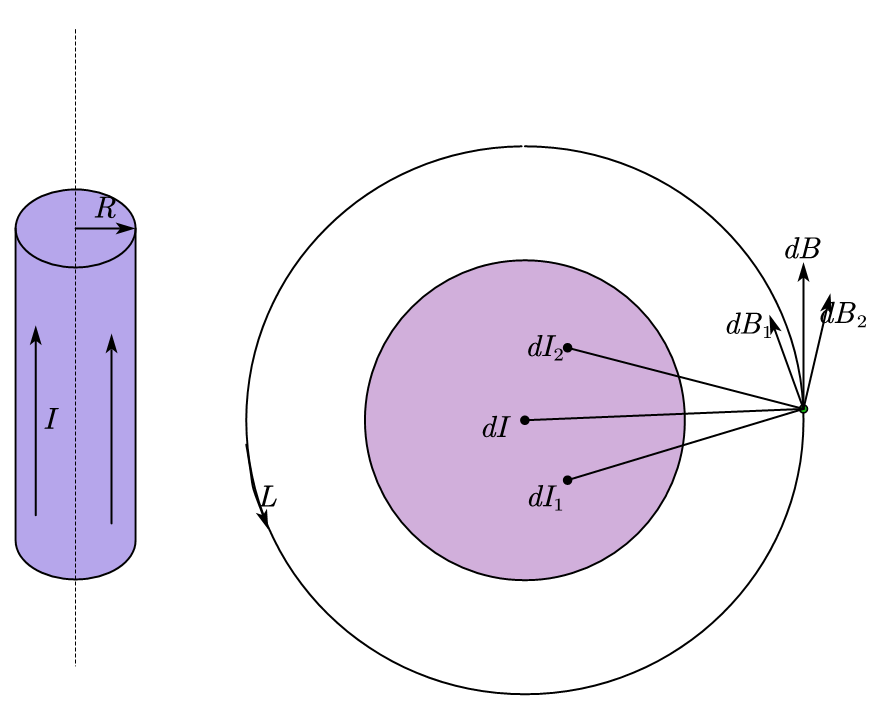$$ \oint_LB\cdot dl=2\pi rB=\mu_0I $$ 所以得到： $$ B=\frac{\mu_0I}{2\pi r} ,r>R $$ 当$rR \end{matrix}\right. $$

$$
空心圆柱：B=
\left{\begin{matrix}
0&,r<R \
\frac{\mu_0I}{2\pi r} & ,r>=R
\end{matrix}\right.
$$

7.2. 长直载流螺线管内的磁场分布

$$
\oint_LB\cdot dl=\int_{AB}B\cdot dl+\int_{BC}B\cdot dl+\int_{CD}B\cdot dl+\int_{DA}B\cdot dl
$$

$$
\int_{AB}B\cdot dl=B\overline{AB}
$$

$$
\because BC、AD垂直与B，而
CD处：B=0
$$

所以可以得到：
$$
\oint_LB\cdot dl=\int_{AB}B\cdot dl=\mu_0I(n\overline{AB})
$$

$$
B=\mu_0nI
$$

7.3. 载流螺绕环的磁分布

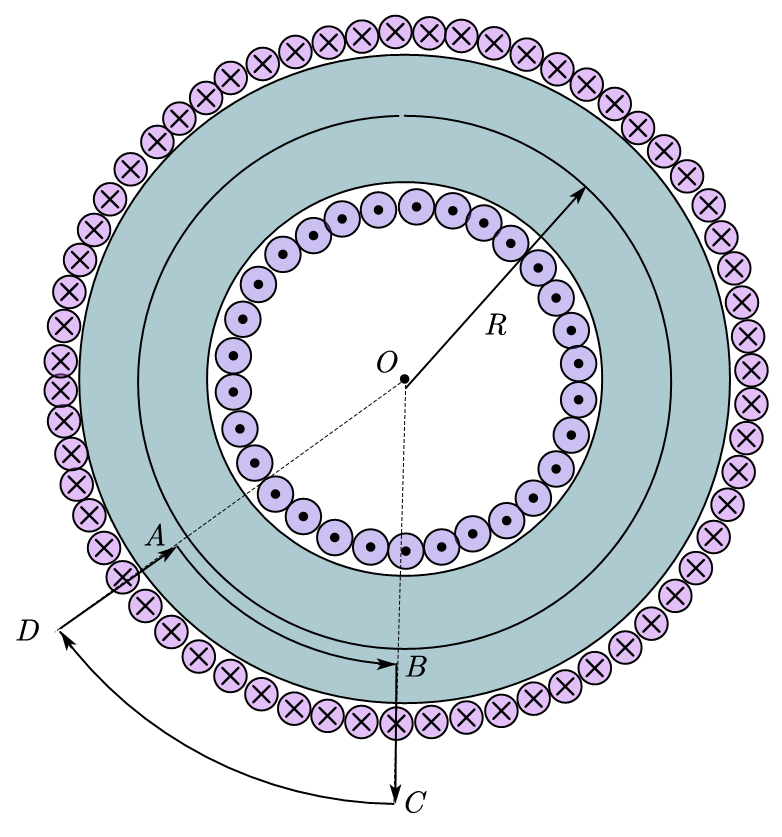
$$
\oint_LB\cdot dl=B\cdot2\pi r=\mu_0NI
$$
所以求得：
$$
B=\frac{\mu_0NI}{2\pi r},R-\frac{d}{2}<r<R+\frac{d}{2}
$$
d为大环半径-小环半径

当环很细的时候，R很大，即R>>d,可认为r约等于R。令$n=\frac{N}{2\pi R}$

所以得：
$$
B=\frac{\mu_0NI}{2\pi R}=\mu_0nI
$$

8. 磁场对运动电荷和载流导线作用

8.1. 洛伦兹力

$$
F=qB\times v = qvBsin\theta
$$

v X B 为方向，由电荷为正，方向不变；电荷为负，方向相反

高中记法：
$$
F=qvB
$$

8.2. 带点粒子在磁场运动

$$
F=qvB=m\frac{v^2}{R}
$$

所以
$$
R=\frac{mv}{qB}
$$

$$
T=\frac{2\pi R}{v_0}=\frac{2\pi m}{qB}
$$

8.3. 应用

• 速度选择器：

$F=Eq=qvB$ 所以有：$V=\frac{E}{B}$

核质比：$\frac{q}{m}$

• 霍尔元件

$I=qnvs$

8.4. 安培力

只与始末位置有关,与路径无关:

高中记法：
$$
F=BIL
$$

$$
F=IL\times B
$$

微分形式：
$$
dF=Idl\times B
$$

$$
F=\int Idl\times B
$$

8.5. 磁力矩

磁矩:
$$
P_m=IS_{en}
$$
磁力矩:
$$
M=P_m\times B
$$

9. 磁力做功

9.1. 长载流直导线

$$
W=F\Delta x=BIL\times\Delta x =I B\Delta S=I\Delta \Phi_m
$$

所以
$$
W=I\Delta \Phi_m
$$
积分形式:
$$
W=\int_{\Phi_{m1}}^{\Phi_{m2}}Id{\Phi_{m}}
$$

10. 介质中磁化强度

为介质产生的磁化强度,不考虑其他
$$
\oint_LM\cdot dl=\sum_{L内}I_s
$$

11. 磁介质中的高斯定理

$$
\oint_SB\cdot dS=0
$$

12. 磁介质中的安培环路定理

$$
\oint_LB\cdot dl=\mu_0(\sum I+\sum_{L内}I_s)
$$

$$
\oint_LB\cdot dl=\mu_0(\sum I+\oint_LM\cdot dl)
$$

所以整理有:
$$
\oint_L(\frac{B}{\mu_0}-M)\cdot dl=\sum I
$$
所以有:
$$
\oint_LH\cdot dl=\sum I
$$
因为:磁化强度=磁化率*总的磁场强度 有:
$$
M=\chi_mH
$$
所以:
$$
B=\mu_0H+\mu_0M=\mu_0(1+\chi_m)H
$$
令:$\mu_r=(1+\chi_m)$ 所以有:
$$
B=\mu_0\mu_rH=\mu H
$$

13. 电磁感应定律

13.1. 法拉第电磁感应定律

右手螺旋

感应电动势:
$$
E=-N\frac{d\Phi_m}{dt}=-N\frac{d(BS)}{dt}
$$

13.2. 楞次定律

增减反同\来拒去留\增缩减阔

阻碍磁场的变化

14. 动生电动势

产生的原因:洛伦磁力
$$
电动势:E_压=\int E_场dl
$$

$$
E_场=\frac{F_{洛}}{q}
$$

$$
F_{洛}=qv\times B
$$

所以有:
$$
E_压=\int (v\times B) dl
$$
高中为$E=Blv$

15. 感生电动势

$$
E=\oint_L E_{感}\cdot dl=-\frac{d \Phi_m}{dt}
$$

又有:
$$
\Phi_m=\iint_SB\cdot dS
$$
所以:
$$
\oint_L E_{感}\cdot dl=-\iint_S\frac{\partial B}{\partial t}\cdot dS
$$

16. 自感

$$
U=-L\frac{dI}{dt}
$$

所以:
$$
L=\frac{\phi}{I} \ \ \ \ \phi为全磁通
$$

$$
L=-U\frac{dI}{dt}
$$

17. 互感

$$
M=\frac{\phi_{21}}{I_1}\ \ \ or\ \ \ M=-U_{21}\frac{dI_1}{dt}
$$

18. 位移电流的引入

$$
\oint_LH\cdot dl=I
$$

但当包括的变为电容后,
$$
I_d=\iint_S\delta_d\cdot dS=\iint_S\frac{\partial D}{\partial t}\cdot dS
$$
则全电流为:
$$
I_{全电流}=I_{传导电流}+I_{位移电流}
$$

$$
\oint_LH\cdot dl=\iint_s\delta_0\cdot dS+\iint_S\frac{\partial D}{\partial t}\cdot dS
$$

19. 麦克斯韦方程组与电磁波

$$
\oint_l H\cdot dl=\iint_s(\delta+\frac{\partial D}{\partial t})\cdot dS
$$

$$
\oint_LE\cdot dl=-\iint_S\frac{\partial B}{\partial t}\cdot dS
$$

$$
\oiint_SD\cdot dS=\sum_Iq_i
$$

$$
\oiint_SB\cdot dS=0
$$

力学

位移速度加速度

微分形式：
$$
v=\frac{dx}{dt}\ \ \ \ \ \ \ \ \ \ \ \ \ 有:x-x_0=\int_0^tvdt
$$

$$
a=\frac{dv}{dt}\ \ \ \ \ \ \ \ \ \ \ \ \ 有:v-v_0=\int_0^tadt
$$

曲率半径

$$
a_n=\frac{v^2}{\rho},所以\rho=\frac{v^2}{a_n}
$$

圆周运动

$$
v=R\omega
$$

$$
\omega =\frac{d\theta}{dt}
$$

$$
\beta=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}
$$

$$
a=a_n+a_t=\frac{v^2}{R}e_n+\frac{dv}{dt}e_t=\omega^2Re_n+R\beta e_t
$$

更多公式在对比公式里面

牛顿运动定律

第一

惯性

第二

$$
F=m\frac{dv}{dt}=ma
$$

第三

$$
F=-F’
$$

万有引力

$$
F_{12}=-G\frac{m_1m_2}{r^2}e_r
$$

重力

$$
G\frac{Mm}{R^2}=mg
$$

所以：
$$
g=G\frac{M}{R^2}
$$

弹簧弹力

$$
f=-k(x_1-x_0)
$$

摩擦力

$$
f=\mu mg
$$

动量及冲量

动量
$$
p=mv
$$
冲量
$$
Fdt=dp
$$
所以积分形式
$$
I=\int_{t_0}^{t}F(t)dt=\int_{p_0}^{p}dp=p-p_0
$$

动量守恒

$$
m_0v_0=m_1v_1+m_2v_2
$$

或有：
$$
Ft=mv-mv
$$

功 、 能

$$
做功：W=Fs
$$

$$
平均功率：\overline{P}=\frac{\Delta W}{\Delta t}
$$

瞬时功率：
$$
P=\frac{dW}{dt}=\frac{d(Fs)}{dt}=Fv
$$
重力做功：
$$
W=mg\Delta h
$$
弹簧弹力做功
$$
W=\int_{x_1}^{x_2}-kxdx=\frac{1}{2}kx_1^2-\frac{1}{2}kx_2^2
$$
万有引力做功
$$
W=\int_{r_1}^{r_2}(-G\frac{Mm}{r^2})dr=GMm(\frac{1}{r_2}-\frac{1}{r_1})
$$
摩擦力做功:
$$
W=\int Fds=\int \mu mgds=\mu mgs
$$

动能定理

$$
E_k=\frac{1}{2}mv^2
$$

$$
W=\frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2
$$

势能

$$
W=-\Delta E_p
$$

重力势能:
$$
E=mgh
$$
弹性势能：
$$
E=\frac{1}{2}k\Delta x^2
$$
万有引力势能：
$$
E=\int_e^\infty (-G\frac{Mm}{r^2})dr=-G\frac{Mm}{r}
$$

机械能守恒

$$
\sum W_外+\sum W_{内非保守}=0
$$

力矩

$$
M=r\times F
$$

角动量

$$
L=r\times p=r\times mv=m\omega r^2
$$

关系：
$$
M=\frac{dL}{dt}\ \ \ \ \ \ \ \ \ \ \ \ \ 角冲量：\int_{t_0}^{t}M dt=L-L_0
$$

角动量守恒

$$
L=r\times p=r\times mv=C_{常数}
$$

角动量定理+守恒

所有的内力矩之和为0

$L=L_0=C_{常数}$

附录

对比使用公式

力矩	$M=FS$
电矩	$P=ql$
磁矩	$P_m=IS_{en}$

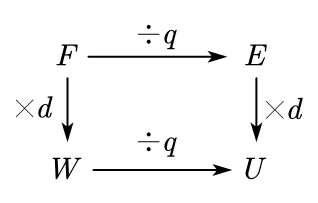
	$F=Eq$
$W=Fd$		$U=Ed$
	$W=qU$

高斯公式
电场		磁场
真空	$\oint _sEdS=\frac{1}{\varepsilon _0}\sum_i q_i$	真空	$\oint _sBdS=0$
有介质	$\oint sDdS=\oint_S \varepsilon_r\varepsilon_0E{介质}\cdot dS= \sum_i q_i$	有介质	$\oint_SB\cdot dS=0$
环路积分
电场	相当于做功	磁场
真空	$\oint_LEqdl=\oint_L Edl=0$	真空	$\oint B\cdot dl=\mu_0\sum_iI_i$
有介质	$\oint_L Edl=0$	有介质	$\oint_LH\cdot dl=\sum I$
$D=\varepsilon_r\varepsilon_0E_{介质}$		$H=\frac{B}{\mu_r\mu_0}$

$$
安培力:F=BIL \洛伦茨力:F=q_0vB\感应电动势:E=BLV
$$

圆周运动
位移	$s$	角度	$\theta$
速度	$v$	角速度	$\omega$
加速度	$\alpha$	角加速度	$\beta$

$x_t=x_0+v_0t+\frac{1}{2}a t^2$	$\theta_t=\theta_0+\omega_0t+\frac{1}{2}\beta t^2$
$v_t=v_0+at$	$\omega_t=\omega_0+\beta t$
$\omega^2-\omega_0^2=2\beta (\theta-\theta_0)$	$v^2-v_0^2=2a (x-x_0)$
$v =\frac{dx}{dt}$	$\omega =\frac{d\theta}{dt}$
$a=\frac{dv}{dt}=\frac{d^2x}{dt^2}$	$\beta=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}$

转换公式：

$v=\omega R$

$a=a_n+a_t=\frac{v^2}{R}e_n+\frac{dv}{dt}e_t=\omega^2Re_n+R\beta e_t$

力：F

力矩：$M=r\times F$

动量：$p=mv$

角动量:$L=r\times p=r\times mv=m\omega r^2$

冲量：$I=\int_{t_0}^{t}F(t)dt=\int_{p_0}^{p}dp=p-p_0$

角冲量：$\int_{t_0}^{t}M dt=L-L_0 $

力矩与角动量:$M=\frac{dL}{dt}$

力与动量:$F=\frac{dp}{dt}$

转动惯量：$$