数学建模
数学建模
数学建模学习
建模方法:
模型假设-建模与求-模型评价-模型改进-模型检验
微分方程建模方法
步骤:
1.要根据问题确定要研究的量,设好所有用到的变量(自变量、未知变量、必要参数),确定坐标系等方法。
2.找到量所满足的基本规律。
3.运用规律列出方程和确定解 使用到导数
1. 按规律直接列方程
例题1:

牛顿冷却定律:温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。当物体表面与周围存在温度差时,单位时间从单位面积散失的热量与温度差成正比,比例系数称为热传递系数。牛顿冷却定律是牛顿在1701年用实验确定的,在强制对流时与实际符合较好,在自然对流时只在温度差不太大时才成立。 是传热学的基本定律之一,用于计算对流热量的多少。
$$
设物体在t时刻温度为u=u(t),牛顿冷却定律得:\frac{du}{dt}=-\frac{u(t)-u(t_\infty )}{\tau }=-k(u-\widetilde{u}) \ \ 其中\widetilde{u}为常温的温度 \ \ k>0 \ 令\widetilde{u}=24 \ \ 且(u-\widetilde{u})>0
$$
则:
$$
\frac{du}{u-24}=-k \ dt \ ==> \frac{d(u-24)}{u-24}=-k \ dt 这里用了积分的性质,积分号里面不变\
求微分:
\int_{150}^{u}\frac{d(u-24)}{u-24}=\int_{0}^{t}-k \ dt \ \ \ \
得:ln(u-24)|{150}^{u} = -kt|{t}^{0} \ \ \
u=24+126e^{-kt}\ \ 带入t=0,u_0=150 \ \ 与 \ \ t=10,u=100 \
得k=0.0506 \ \ \ \ 所以u=24+126e^{-0.0506t}
$$
1 | import sympy as sp |
2. 微元分析法
例题2:

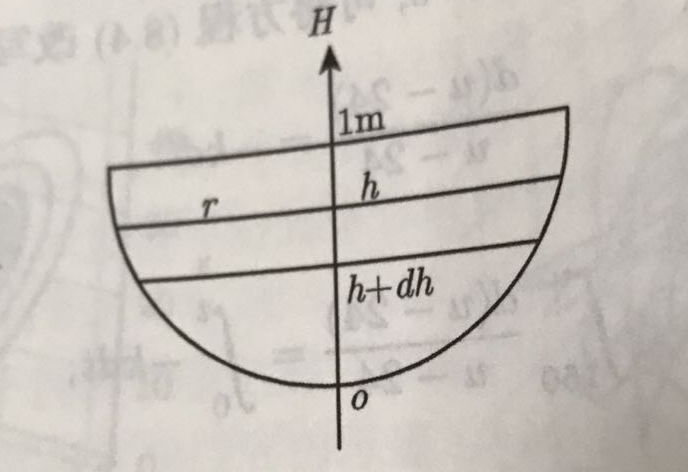
设流量为Q 通过孔的水的体积V 时间t g为重力加速度(9.8m/s2) 0.62为流量系数 h为高cm S为孔的面积cm2
流量系数:是指单位时间内、在测试条件中管道保持恒定的压力,管道介质流经阀门的体积流量,或是质量流量。 即阀门的流通能力。 流量系数值越大说明流体流过阀门时的压力损失越小。
得到公式为:
$$
Q=\frac{dV}{dt}=0.62S\sqrt{2gh}
$$
同一单位后:
$$
dV=0.000062S\sqrt{2gh}\ dt
$$
在微小的一段时间里面:[t , t+dt ] 内,高度变化 [ h , h+dh ] ( dh<0 ) , 容器中水的体积的改变:
$$
dV = - \pi r^2 \ dh \
r为液面的半径\ \ \ \ R为球的半径\ \ \ \ h 为液面的高度 \
r^2 = [R^2-(R-h)^2]=2h-h^2
$$
所以带入r2=2h-h2
$$
0.000062 \sqrt{2gh}\ dt = -\pi (2h-h^2)\ dh
$$
回到题目求 高度h 与 时间t 的变化:
$$
\begin{equation}
\left{
\begin{array}{lr}
\frac{dt}{dh}=\frac{-\pi (2h-h^2)}{0.000062 \sqrt{2gh}} \
h(0)=1
\end{array}
\right.
\end{equation} \
$$
$$
{\color{Red}eq} = \frac{dt}{dh}-\frac{-\pi (2h-h^2)}{0.000062 \sqrt{2gh}}=\color{Red}\frac{dt}{dh}-\frac{1000000\pi (h^{\frac{3}{2}}-2h^{\frac{1}{2}})}{62 \sqrt{2g}}
$$
1 | import sympy as sp |
所以方程的解为:
$$
\color{Red}t(h)=-15260.5042h^{\frac{3}{2}}+4578.1513h^{\frac{5}{2}}+10682.3530
$$
3. 模拟近似法
例3 (交通管理问题)在交通十字路口,都会设置红绿灯。为了让那些正行驶在交叉路口太近而无法停下的车辆通过路口,红绿灯转换中间还要亮起一段时间的黄灯。那么,黄灯应亮多长时间才最为合理?
首先考虑问的是黄灯亮多长时间,则要考虑:司机反应时间+刹车距离的时间+车通过交叉入口的时间。
首先设:v0是法定速度 I是交通路口长度 L是车长
则:车通过路口的正常时间为:(I+L)/v0
求 开始刹车到速度为0 的距离。
设: W 为汽车的重量 μ为摩擦系数 所以摩擦力为f=μW 方向与运动方向相反
$$
f=μW \ \ \ \ \ W=mg \ \ \ \ \ f=-ma=-m\frac{dv}{dt}=-\frac{W}{g}\frac{d^2 x}{dt^2} \
μmg=-\frac{W}{g}\frac{d^2 x}{dt^2}\
{\color{Red}-μg=\frac{d^2 x}{dt^2}}\
$$
所以得到:
$$
\begin{equation}
\left{
\begin{array}{lr}
-μg=\frac{d^2 x}{dt^2} \
x|{t=0}=0, \ \frac{dx}{dt}|{t=0}=v_0
\end{array}
\right.
\end{equation} \
$$
化简并积分
$$
d^2 x=-μgdt^2 \ \
\int_{0}^{x} d^2 x = \int_{0}^{t}-μgdt^2
$$
得:
$$
\frac{dx}{dt}=-μgt+v_0 \ \ \
$$
二次积分:
$$
\int_{0}^{x}dx = \int_{0}^{t}(-μgt+v_0)dt\
$$
得:
$$
{\color{Red}x(t)=-\frac{1}{2}μgt^2+v_0t}
$$
当利用前面的公式:
$$
\frac{dx}{dt}=0 \ \ \ \ \ \ 和 \ \ \ \ \ \frac{dx}{dt}=-μgt+v_0
$$
得到:
$$
-μgt+v_0=0
$$
所以 刹车所用时间为:
$$
t_0=\frac{v_0}{μg}
$$
然后将时间带入x(t)的公式:
$$
x(t_0)=-\frac{1}{2}μgt^2 |_{t_0=\frac{v_0}{μg}}
$$
所以刹车距离为:
$$
{\color{Red}x(t_0)=}-\frac{1}{2}μg\frac{v_0^2}{μ^2g^2}=\color{Red}-\frac{v_0^2}{2μg}
$$
计算黄灯的时间T:黄灯的时间
$$
T=\frac{x(t_0)+I+L}{v_0}+T_0
$$
总路程为x(t0)+I+L + T0 反应时间 x(t0) 得:
$$
T=\frac{I+L}{v_0}+T_0+\frac{v_0}{2μg}
$$
取μ=0.7 T0=1s L=4.5m I=9m 令:v0 =45km/h 65km/h 80km/h
| v0 / (km/h) | 45 | 65 | 80 |
|---|---|---|---|
| T / s | 4.58 | 5.95 | 7.00 |
1 | from numpy import array |
Lorenz模型的混沌效应
Lorenz模型是由美国气象学家Lorenz在研究大气运动时,通过简化对流模型,只保留3个变量提出的一个完全确定性的一阶自治常微分方程组(不显含时间变量),其方程为
$$
\begin{cases}
& \overset{.}{x}= \sigma(y-x)\
& \overset{.}{y}= \rho x-y-xz\
& \overset{.}{z}= xy-\beta z
\end{cases}
$$
其中,参数σ 为Prandtl数,ρ为Rayleigh数,β为方向比.
第一个混沌吸引子——Lorenz吸引子也是在这个系统中被发现的. 系统中三个参数的选择对系统会不会进入混沌状态其着重要的作用.
蝴蝶效应: σ = 10 ρ = 28 β = 8/3
给出了系统从两个靠得很近的初值出发(相差仅0.0001)后,解的偏差演化曲线. 随着时间的增大,可以看到两个解的差异越来越大,这正是动力学系统对初值敏感性的直观表现,由此可断定此系统的这种状态为混沌态. 混沌运动是确定性系统中存在随机性,它的运动轨道对初始条件极端敏感.
1 | from scipy.integrate import odeint |
Malthus模型
1789年,英国神父Malthus在分析了一百多年人口统计资料之后,提出了Malthus模型.
1.模型假设
- 设x(t)表示t时刻的人口数,并且x(t)连续且可微
- 设人口的增长率r是常数(增长率 = 出生率 - 死亡率)
- 人口的变化封闭,人口数量的增加与减少只取决于人口中个体的生育和死亡,且每一个体都具有同样的生育能力与死亡率。
2.建模与求解
设:t->t+Δt 人口的增量为:x(t+Δt) - x(t) = r x(t) Δt
$$
\begin{cases}
& \frac{dx}{dt}=rx \ \ \ \ \ \ 增长的人数=增长率*总人口\
& x(0)=x_0 \ \ \ 初始人口为一定值
\end{cases}
$$
求解:
$$
\int_{0}^{x}\frac{1}{x}dx=\int_{0}^{t}r\ dt
$$
所以:
$$
lnx|_0^x=rt|^t_0
$$
解的:
$$
lnx-lnx_0=ln\frac{x}{x0}=rt
$$
所以:
$$
\frac{x}{x_0}=e^{rt}
$$
方程的解为:
$$
x(t)=x_0\ e^{rt}
$$
3.模型评价
考虑二百多年来人口增长的实际情况,1961年世界人口总数为3.06x109,在1961~1970年这段时间内,每年平均人口自然增长率为2%,则带入上式有:
$$
x(t)=3.06\times 10^9\cdot e^{0.02(t-1961)}
$$
因为在这期间地球人口大约每35年增加1倍,而(3) 式算出每34.6年增加1倍.短期内,计算结果相当符合事实。但当t=2670年时,x(t)=4.4x1015,即4400万亿,相当于地球没平方米容纳至少20人。显然是不对的, 误差的原因是增长率r的估计过高,由此,可以队r这个常数提出假设。
4.模型改进
一、 当增长率不是常数时的模型**
因为地球资源是有限的,他只提供一定量的生命生存所需的条件。人口增加,自然资源、环境资源等会对人口再增长的限制越来月显著。当人过少时,可以r看为常数,但一定量后,r随着人口的增加而减少,即增长率r表示为x(t)的函数r(x(t)),记为r(x),且r(x)为x的减函数。
模型再次假设
- 设r(x)为x的线性函数,r(x)= r - sx (工程署原则,首先用线性)
- 自然资源与环境条件所能容纳的最大人口数为xm,当x=xm时,增长率r(xm)= 0
模型建立与求解
由公式这个:
$$
\frac{dx}{dt}=rx
$$
可以想到斜率会是s型。那么:
$$
令r(x)=r(1-\frac{x}{x_m}) \ 保证了x大于x_m时会负增长 \ x=x_m时0增长 \
而且增长率虽人口增加而减少
$$
假设了一个增长率函数,然后求解:
$$
\begin{cases}
& \frac{dx}{dt}=r(1-\frac{x}{x_m})x \
& x(t_0)=x_0
\end{cases}
$$
对第一个求积分并化简
$$
\int_{0}^{x}\frac{1}{(1-\frac{x}{x_m})x}dx=\int_{0}^{x}\frac{x_m}{xx_m-x^2}dx=\int_{0}^{t}r\ dt \ \ \ \ \ \ \ \ \ \ \ \ (x_m为定值)
$$
求解:
$$
x(t)=\frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-r(t-t_0)}}
$$
这个就是Logistic模型
模型检验
$$
\frac{dx}{dt}求导得:\frac{d^2x}{dt^2}=r^2(1-\frac{x}{x^m})(1-\frac{2x}{x_m})x
$$
人口总数x(t)有如下规律:
$$
\lim_{t\rightarrow\infty}x(t)=x_m \ \ \ \ \ \ \ \ \ \ \ \ 即无论人口初值 如何,人口总数以 为极限.
$$
$$
当0<x_0<x_m时,\frac{dx}{dt}=r(1-\frac{x}{x_m})x > 0 \ \ \ 说明x(t)是单调增加的;
$$
$$
当x<\frac{x_m}{2}时,\frac{d^2x}{dt^2}>0,x=x(t)为凹函数
$$
$$
当x>\frac{x_m}{2}时,\frac{d^2x}{dt^2}<0,x=x(t)为凸函数
$$
$$
人口变化率\frac{dx}{dt}在x=\frac{x_m}{2}时取最大值 \即人口总数达到极限值一半以前是加速生长,过了这一点后,会逐渐减小,最终达到0。
$$
例题
利用下表给出的近两个世纪的美国人口统计数据(以百万为单位),建立人口预测模型,最后用它估计2010年美国的人口。
| 年份 | 1790 | 1800 | 1810 | 1820 | 1830 |
|---|---|---|---|---|---|
| 人口 | 3.9 | 5.3 | 7.2 | 9.6 | 12.9 |
| 年份 | 1840 | 1850 | 1860 | 1870 | 1880 |
| 人口 | 17.1 | 23.2 | 31.4 | 38.6 | 50.2 |
| 年份 | 1890 | 1900 | 1910 | 1920 | 1930 |
| 人口 | 62.9 | 76.0 | 92.0 | 106.5 | 123.2 |
| 年份 | 1940 | 1950 | 1960 | 1970 | 1980 |
| 人口 | 131.7 | 150.7 | 179.3 | 204.0 | 226.5 |
| 年份 | 1990 | 2000 | |||
| 人口 | 251.4 | 281.4 |
建立模型与求解
记x(t)为第t年的人口数量,设人口年增长率r(x)为x的线性函数,r(x) = r - sx , 自然资源与环境条件所容纳的最大人口数为xm,即当x = xm时,增长率r(xm) = 0 ,得
$$
r(x)=r(1-\frac{x}{x_m})
$$
建立 Logistic 人口模型:
$$
\begin{cases}
& \frac{dx}{dt}=r(1-\frac{x}{x_m})x \
& x(t_0)=x_0
\end{cases}
$$
解的:
$$
x(t)=\frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-r(t-t_0)}}
$$
参数估计
非线性最小二乘法
将第一个数据为初始条件,用余下的数据来拟合 Logistic 函数的参数xm和r 。解的r=0.0274,xm=342.4419
带入公式得:
$$
x(t)=\frac{342.4419}{1+(\frac{342.4419}{x_0}-1)e^{-0.0274(t-t_0)}}
$$
将数据2010年的数据带入预测值为:2010—-282.6798(百万)
1 | #非线性最小二乘法 |
线性最小二乘法
简单的线性最小二乘估计这个模型的参数 xm 和 r ,把Logistic方程表示为:
$$
\frac{1}{x}\frac{dx}{dt}=r-sx \ \ \ \ ,\ \ \ s=\frac{r}{x_m}
$$
记1790,1800,…… ,2000年分别用 k = 1,2,3,……,21 表示,利用向前差分,得到差分方程:
$$
\frac{1}{x(k)}\cdot \frac{x(k+1)-x(k)}{\Delta t}=r-sx(k)\ \ \ \ \ ,\ \ \ \ \ \ k=1,2,3,…,21
$$
其中步长Δt=10。拟合数据,求得r=0.0325,x(m)=294.3860 ,再求得2010年人口预测值为277.9634百万。
1 | #线性最小二乘法 |
传染病模型
传染病动力学是用数学模型研究某种传染病在某的一地区是否蔓延下去,成为当地的“地方病”,或最终该病将被消除. 下面以Kermack和Mckendrick 提出的阈值模型为例说明传染病动力学模型的建模过程。
模型假设
被研究人群是封闭的,总人数为 n 。s(t) , i(t) , r(t) 分别代表:t 时刻 易感染着、已感染着、免疫者。 起始条件:s0个易感染者 , i0 个感染者 ,n-s0 - i0 个
易感染人数的变化率与当时的易感染人数和感染人数之积成正比 , 系数为 λ。
免疫者人数的变化率与当时的感染者人数成正比,比例系数为 μ 。
三类人总的变化率代数和为零.
模型建立
根据上述假设,可以建立如下模型:
$$
\begin{cases}
& \frac{ds}{dt}= -\lambda si\
& \frac{dr}{dt}= \mu i\
& \frac{di}{dt}+\frac{ds}{dt}+\frac{dr}{dt}=0 \
& \frac{di}{dt}= \lambda si-\mu i\
& s(t)+i(t)+r(t)=n
\end{cases}
$$
模型又称Kermack-Mckendrick方程
模型求解与分解
上面的方程无法求解出任何一个 s(t) , i(t) , r(t) 的解析解。转到平面 s-i 讨论解的性质。
$$
由 得:\begin{cases}
\frac{di}{ds}=\frac{1}{\sigma s}-1\
\sigma=\frac{\lambda}{\mu}\
i|_{s=s_0}=i_0 \
\end{cases}
$$
$$
\mu是易感人数的变化率系数、\lambda是免疫者人数的变化率系数、\sigma则为一个传染期内每个患者有效接触的平均人数
$$
则σ为接触数.
分离变量法求解:
$$
di=(\frac{1}{\sigma s}-1)ds
$$
然后对两边积分:
$$
\int_{i_0}^{i}di=\int_{s_0}^{s}(\frac{1}{\sigma s}-1)ds
$$
得:
$$
i|{i_0}^{i}=(\frac{1}{\sigma}lns-s)|{s_0}^{s}
$$
所以:
$$
i-i_0 =\frac{1}{\sigma}lns-s-\frac{1}{\sigma}lns_0+s_0
$$
化简:
$$
i=i_0+s_0-s+\frac{1}{\sigma}(lns-lns_0)
$$
解的:
$$
i=i_0+s_0-s+\frac{1}{\sigma}(ln\frac{s}{s_0})
$$
由公式得知:
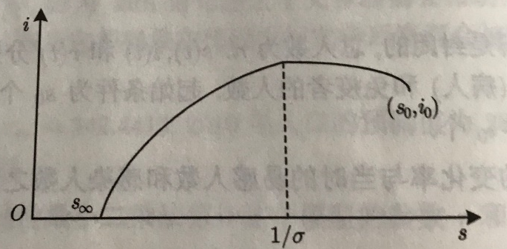
当初始值s0 ≤ 1/ σ 时,患者人数会增加,传染病开始蔓延,健康者的人数在减少。
当初始值s(t) 减少至 1/ σ 时,患者在人群中的比例达到最大值,然后患者数逐渐减少至零
1/ σ 是阈值,所以要想控制传染病的流行,应控制s0 使之小于阈值.
总结
- 提高卫生和医疗水平,卫生水平越高,使传染性接触率 λ 就越小;医疗水平越高,恢复系数 μ 就越大。
这样子就提高了1/ σ 阈值 。提高卫生和医疗水平有助于控制传染病的蔓延
- 降低s0来控制传染病的蔓延. 由 s0 + i0 + r0 = n 可知道,减少s0可以通过提高r0 来实现。
参数估计
参数σ 的值可由实际的数据估计得:
$$
令s_\infty 与 i_\infty 分别是传染病流行结束后的 健康者人数 和 患者人数。
$$
当流行结束后,患者都将转化为免疫者
$$
i_\infty = 0 \ ;\ \therefore i_\infty=i_0+s_0-s_\infty+\frac{1}{\sigma}(ln\frac{s_\infty}{s_0}),
$$
解的:
$$
\sigma=-\frac{lns_0-lns_\infty}{s_\infty-i_0-s_0}
$$
于是,当已知某地区某种传染病流行结束后的 $s_\infty$ 时,则可以算出 $\sigma$ , $\sigma$ 值可再今后同种传染病和同类地区的研究中使用。
例题
1950年上海市某全托幼儿所发生的一起水痘流行过程中各代病例数、易感染者数及间隔时间如下,应用K-M模型进行模拟,并对模拟结果进行讨论. 该所儿童总人数n 为196人;既往患过水痘而此次未感染者40人,查不出水痘患病史而本次流行期间感染水痘者96人,既往无明确水痘史,本次又未感染的幸免者60人. 全部流行期间79人,病例成代出现,每代间隔约15人.
| 代 | 病例数 | 易感染者 | 间隔时间/天 |
|---|---|---|---|
| 1 | 1 | 155 | |
| 2 | 2 | 153 | 15 |
| 3 | 14 | 139 | 32 |
| 4 | 38 | 101 | 46 |
| 5 | 34 | 67 | |
| 6 | 7 | 33 | |
| 合计 | 96 |
以初始值s0,$s_\infty$代入$\sigma=-\frac{lns_0-lns_\infty}{s_\infty-i_0-s_0}$ 可得 $ \sigma=0.0099 $ .
将代入$i=i_0+s_0-s+\frac{1}{\sigma}(ln\frac{s}{s_0})$ 可得该流行过程的模拟结果如下表2.
| 易感染者 | 155 | 153 | 139 | 101 |
|---|---|---|---|---|
| 病例数i | 1 | 1.7 | 6.0 | 11.7 |
程序
1 | import numpy as np |
插值与拟合
在数学建模过程中,通常要处理由试验、测量得到的大量数据或一些过于复杂而不方便计算的函数表达式,针对此情况,很自然的想法就是,构造一个简单的函数作为要考察数据或复杂函数的近似. 插值和拟合就可以解决这样的问题
给定一组数据,需要确定满足特定要求的曲线(或曲面),如果所求曲线通过所给定的有限个数据点,这就是插值. 有时由于给定的数据存在测量误差,往往具有一定的随机性. 因而,通过所有数据点求曲线不现实也不必要. 如果不要求曲线通过所有数据点,而是要求它反映对象整体的变化态势,得到简单实用的近似函数,这就是拟合.
拟合函数的选择
数据拟合时,首要也是最关键的一步就是恰当的拟合函数. 如果能够根据问题的背景通过机理分析得到变量之间的函数关系,那么只需估计相应的参数即可. 但很多情况下,问题的机理并不清楚. 此时,一个较为自然的方法是先做出数据的散点图,从直观上判断应选用什么样的拟合函数.
如果数据分布接近于直线,则拟合函数宜选用线性函数 $f(x)=a_1x+a_2$ ;
如果数据分布接近于抛物线,则拟合函数宜选用二次多项式 $f(x)=a_1x^2+a_2x+a_3$ ;
如果数据分布特点是开始上升较快随后逐渐变缓,则宜选用双曲线型函数或指数型函数,即用 $f(x)=\frac{x}{a_1x+a_2}$ 或 $ f(x)=a_1e^{-\frac{a_2}{x}}$ ;
如果数据分布特点是开始下降较快随后逐渐变缓,则宜选用$f(x)=\frac{1}{a_1x+a_2}$,$f(x)=\frac{1}{a_1x^2+a_2}$ , $f(x)=a_1e^{-a_2x}$
常被选用的非线性拟合函数有$y=a_1+a_2\ lnx$ ,S形曲线函数为$y=\frac{1}{a+be^{-x}}$
数据拟合python程序实现:
python中有多个模块的多种方法可以进行拟合未知参数.
Numpy中的多项式拟合函数polyfit
Scipy.optimize中的leastsq(最小二乘)、curve_fit
例题一
对下表1的数据进行拟合,并求当x=0.25 ,0.35 时, y的预测值.
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| y | -0.447 | 1.978 | 3.28 | 6.16 | 7.08 | 7.34 | 7.66 | 9.56 | 9.48 | 9.30 | 11.2 |
解:
1 | #显示点 |
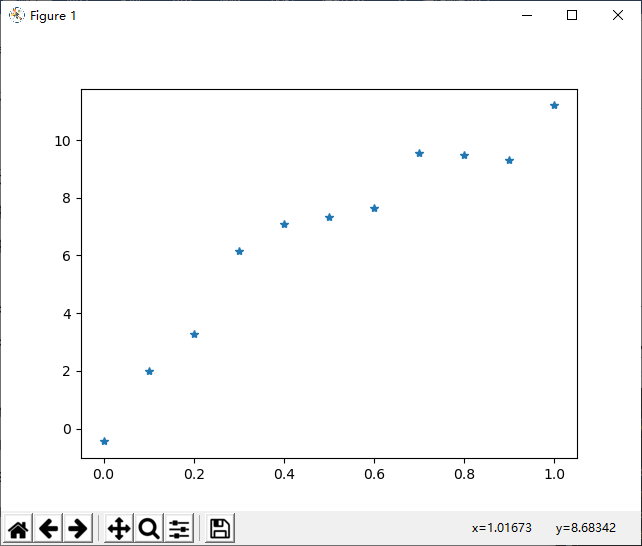
可以看出,接近于直线或抛物线.这里抛物线更加准确.
1 | import numpy as np |
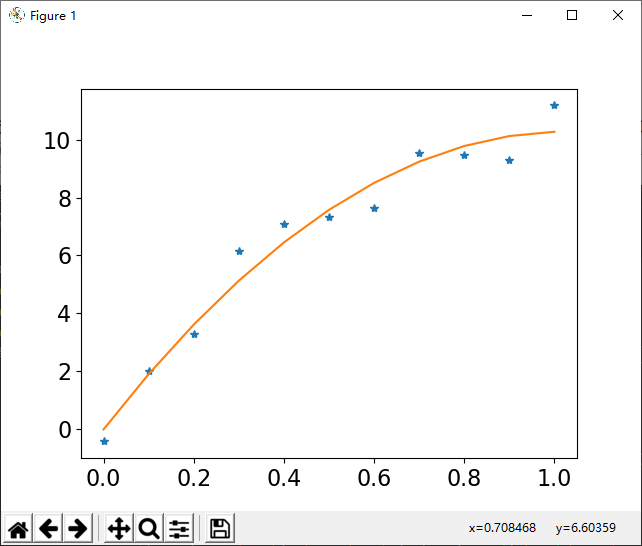
拟合二次多项式的从高次幂到低次幂系数分别为: [-9.81083916 20.12929371 -0.03167133]
预测值分别为: [4.38747465 5.81175367]
例题二
对例1的数据用 curve_fit 函数拟合二次多项式,并求预测值
1 | import numpy as np |
例题三
用下标数据拟合二元函数 : $z=ae^{bx}+cy^2$
| x | 6 | 2 | 6 | 7 | 4 | 2 | 5 | 9 |
|---|---|---|---|---|---|---|---|---|
| y | 4 | 9 | 5 | 3 | 8 | 5 | 8 | 2 |
| z | 5 | 2 | 1 | 9 | 7 | 4 | 3 | 3 |
1 | import numpy as np |
例题四
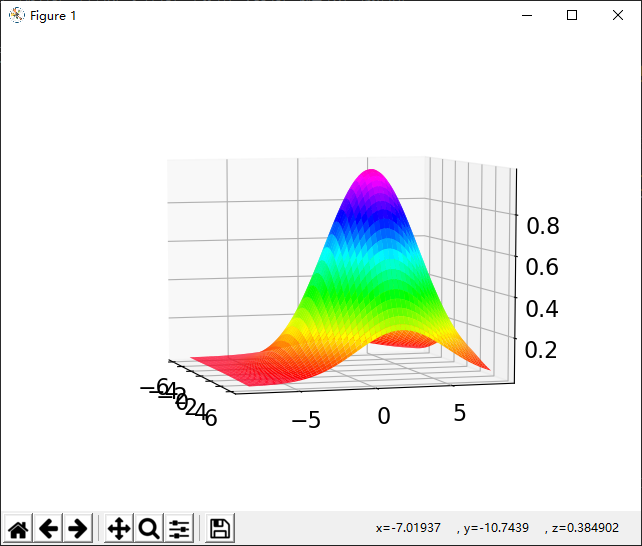
利用模拟数据拟合曲面 $z=e^{-\frac{(x-\mu_1)^2+(y-\mu_2)^2}{2\sigma^2}}$ , 并画出拟合曲面的图形
其中$\mu_1=1$,$\mu_2 =2$,$\sigma=3$,生成加噪声的模拟数据$\mu_1=1.0097$,$\mu_2 =1.9968$,$\sigma=3.0028$
画出拟合曲面:
1 | from mpl_toolkits import mplot3d |
数学建模之回归分析
多元线性回归模型
通过对变量实际观测的分析、计算,建立一个变量与另一组变量的定量关系即回归方程,经统计检验认为回归效果显著后,可用于预测与控制
设随机变量 $y$ 与变量 $x_1,x_2,…,x_m$ 有关则其 $m$ 元线性回归模型为:
$$
y=\beta_0+\beta_1x_1+…+\beta_mx_m+\varepsilon
$$
$\varepsilon$是随机误差服从正态分布 $N(0,\sigma^2)$ ,$\beta_0,\beta_1,…,\beta_m$ 为回归系数。
主要步骤
由观察确定回归系数
$\beta_0,\beta_1,…,\beta_m$ 的估计值 $b_0,b_1,…,b_m$
将 $n$ 组数据 $(y_i,x_{i1},..,x_{im})$ ,$i=1,…,n (n>m)$ 带入 $y=\beta_0+\beta_1x_1+…+\beta_mx_m+\varepsilon$ 有
$$
y_i=\beta_0+\beta_1x_{i1}+…+\beta_mx_{im}+\varepsilon_i
$$
$$
记\ \ X=
\begin{bmatrix}
1 & x_{11} & x_{12} & \cdots & x_{1m}\
1 & x_{21} & x_{22} & \cdots & x_{2m}\
\vdots & \vdots & \vdots & \ddots & \vdots \
1 & x_{n1} & x_{n2} & \cdots & x_{nm}
\end{bmatrix},
Y=
\begin{bmatrix}
y_{1} \
y_{2} \
\vdots \
y_{n}
\end{bmatrix},
\varepsilon=
\begin{bmatrix}
\varepsilon_1 \ \varepsilon_2 \ \cdots \varepsilon_n
\end{bmatrix}^T,
\beta=
\begin{bmatrix}
\beta_1 \ \beta_2 \ \cdots \beta_n
\end{bmatrix}^T.
$$
则正规方程组为:$Y=X \ \beta + \varepsilon$ , 正规方程组的回归系数的最小二乘法估计 $\hat{\beta}$ 为:
$$
\hat{\beta} = (X^TX)^{-1}X^TY
$$
将$\hat{\beta}=[b_0,b_1,…,b_m]$ 带入$y=\beta_0+\beta_1x_1+…+\beta_mx_m+\varepsilon$ 得到方程:
$$
y=b_0+b_1x_1+…+b_mx_m
$$
将数据代入,则得 $y$ 的估计值:
$$
\hat{y} = b_0+b_1x_1+…+b_mx_m
$$
估计值的残差平方和为:
$$
SSE=\sum_{i=1}^{n}e_i^2=\sum_{i=1}^{n}(y_i-\hat{y_i})^2
$$
回归平方和为:
$$
SSR=\sum_{i=1}^{n}(\overline{y}-\hat{y_i})^2
$$
对线性关系、自变量的显著性进行统计检验
上面完美建立的线性回归方程是假定了变量$y$与$x_1,x_2,…,x_m$ 是有关系的,但真的是否有线性关系吗?需要做统计检验。
首先,因变量 $y$ 与 自变量$x_1,x_2,…,x_m$ 之间关系的检验方式,令原假设成立:
$$
H_0:\beta_1=\beta_2=…=\beta_m=0
$$
选择统计量$F=\frac{SSR/m}{SSE/(n-m-1)}=\frac{SSR\cdot(n-m-1)}{SSE\cdot m}$~$F(m,n-m-1)$ 进行假设检验,对显著性水平$\alpha$ 和上分位数$F_\alpha(m,n-m-1)$ ,检验准则为:
若 $ F>F_\alpha(m,n-m-1)$,回归方程显著。
若 $ F<F_\alpha(m,n-m-1)$,回归方程效果不显著。
也可以采用复判定系数(也称拟合优度) $R^2=\frac{SSR}{SSR+SSE}$ 作为权衡 $y$ 与 $x_1,x_2,…,x_m$ 相关程度的指标,$R=\sqrt{R^2}$成为复相关系数,R越大, $y$ 与 $x_1,x_2,…,x_m$ 相关关系越密切,通常R>0.8/0.9才认为相关关系成立。
利用回归方程进行预测
对于给定的$x_1^{(0)},x_2^{(0)},…,x_m^{(0)},$ 代入回归方程: $y=b_0+b_1x_1+…+b_mx_m $ 得:
$$
\hat{y_0} = b_0+b_1x_1^{(0)}+…+b_mx_m^{(0)},
$$
用 $\hat{y_0}$做 $y$ 在点$x_1^{(0)},x_2^{(0)},…,x_m^{(0)}$ 的预测值。
也可以进行区间的估计,记$s=\sqrt{\frac{SSE}{n-m-1}} , x_0=[1,x_1^{(0)},x_ 2^{(0)},…,x_m^{(0)}]$ , 则$y_0$的置信度为$1-\alpha$ 的车预测区间为:
$$
(\ \hat{y}-t_{1-\alpha/2}(n-m-1)s\sqrt{1+x_0^T(X^TX)^{-1}x_0}\ ,\ \hat{y}+t_{1-\alpha/2}(n-m-1)s\sqrt{1+x_0^T(X^TX)^{-1}x_0}\ )
$$
例题一:
水泥凝固时放出的热量 y 与水泥中两种主要化学分成 x1,x2 有关,今测得一组数据如表1所示,试确定一个线性回归模型$y=a_0+a_1x_1+a_2x_2$.
| 序号 | $x_1$ | $x_2$ | $y$ | 序号 | $x_1$ | $x_2$ | $y$ |
|---|---|---|---|---|---|---|---|
| 1 | 7 | 26 | 78.5 | 8 | 1 | 31 | 72.5 |
| 2 | 1 | 29 | 74.3 | 9 | 2 | 54 | 93.1 |
| 3 | 11 | 56 | 104.3 | 10 | 21 | 47 | 115.9 |
| 4 | 11 | 31 | 87.6 | 11 | 1 | 40 | 83.8 |
| 5 | 7 | 52 | 95.9 | 12 | 11 | 66 | 113.3 |
| 6 | 11 | 55 | 109.2 | 13 | 10 | 68 | 109.4 |
| 7 | 3 | 71 | 102.7 |
程序一:利用模块sklearn.linear_model中的函数LinearRegression求解
解:求得回归模型为
$$
y=52.5773+1.4683x_1+0.6623x_2
$$
模型的拟合优度$R^2=0.9787$,说明拟合效果很好.
1 | import numpy as np |
线性回归模型的正则化求解
在多元线性回归中,解释变量$x_1,x_2,…,x_m$之间出现严重的多重线性时,普通的最小二乘法估计模型参数,往往参数估计方差太大,使普通最小二乘法的效果很不理想. 为改进线性回归模型,采用线性回归正则化方法,岭回归和Lasso回归是其中的两种方法
这里我认为是机器学习中次方过大,导致过拟合,于是得到的函数干扰太大拟合效果不好。
法一:岭回归
例题
Malinvand于1966年提出的研究法国经济问题的一组数据,如下表1. 所考虑的因变量为进口总额y , 三个解释变量分别为:国内总产值x1、储存量x2、总消费x3(单位均为10亿法郎). 建立y与x1、x2、x3的关系
| 年份 | $x_1$ | $x_2$ | $x_3$ | $y$ | 年份 | $x_1$ | $x_2$ | $x_3$ | $y$ |
|---|---|---|---|---|---|---|---|---|---|
| 1949 | 149.3 | 4.2 | 108.1 | 15.9 | 1955 | 202.1 | 2.1 | 146.0 | 22.7 |
| 1950 | 171.5 | 4.1 | 114.8 | 16.4 | 1956 | 212.4 | 5.6 | 154.1 | 26.5 |
| 1951 | 175.5 | 3.1 | 123.2 | 19.0 | 1957 | 226.1 | 5.0 | 162.3 | 28.1 |
| 1952 | 180.8 | 3.1 | 126.9 | 19.1 | 1958 | 231.9 | 5.1 | 164.3 | 27.6 |
| 1953 | 190.7 | 1.1 | 132.1 | 18.8 | 1959 | 239.0 | 0.7 | 167.6 | 26.3 |
| 1954 | 202.1 | 2.2 | 137.7 | 20.4 |
用最小二乘估计建立模型
对于上述问题,可以直接用普通的最小二乘估计建立$y$关于三个解释变量x1、x2、x3 的回归方程为$y=-8.6203-0.0742x_1+0.5104x_2+0.3116x_3$ , 并且模型的统计检验指标都相当好,但是$x_1$的系数为负数,这是不符合经济意义的,因为法国是一个原材料进口国,当国内总产值$x_1$增大时,进口总额$y$肯定也会增加,所以符号应该时正的。原因可能是三个自变量x1、x2、x3 之间存在多重共线性。
计算$x_1,x_2,x_3$的相关系数矩阵为:
$$
R=
\begin{pmatrix}
1 & -0.0329 & 0.9869\
-0.0329 & 1 & 0.0357\
0.9869 & 0.0357 & 1
\end{pmatrix}
$$
可以看到$x_1\text{与}x_2$的相关系数高达0.9869,说明$x_1与x_3$基本线性相关,若将$x_3$看为因变量,$x_1$看作解释变量,那么$x_3$关于$x_1$的一元线性回归方程为:
$$
x_3=-4.9632+0.7297x_1
$$
说明$x_3与x_1$之间存在着多重共线性关系。
利用statsmodels库求解线性回归分析
1 | 基于数组构建并拟合模型的调用格式为: |
程序:
1 | import numpy as np |
1 | $ print(md.summary()) #这一步中输出为: |
改进的模型:岭回归方程
为了消除变量之间的多重共线性关系的影响,即消除最小二乘解的参数估计$\hat{\beta} = (X^TX)^{-1}X^TY中X^TY的奇异性$,采用岭回归模型,即参数估计为:
$$
\hat{\beta} (k)= (X^TX+kI)^{-1}X^TY
$$
其中,k是岭参数. 岭参数的选择有岭迹法和均方误差法.
求上面那道例题的岭回归方程:
我们可以解得k=0.15时,取得较好的拟合效果。对应的标准化岭回归方程为:
$$
\hat{y}^*=0.0610x_1+0.2179x_2+0.8926x_3
$$
将标准化的回归方程还原后得:
$$
\hat{y}=-9.5320+0.0410x_1+0.6231x_2+0.1520x_3
$$
拟合优度为 0.9899
1 | import numpy as np |
lasson 回归
数学原理简介
多元回归中的普通最小二乘法是拟合参数向量$\beta$,使得$\left |X\beta-Y \right |^2_2$达到最小值. 岭回归是选择了合适的参数$k\geq 0$ ,拟合参数向量$\beta$ ,使得$\left |X\beta-Y \right |^2_2-\left |k\beta \right |^2_2$达到最小值,解决了$X^TX$不可逆的问题. Lasso回归,是选择合适的参数$k\geq 0$ ,拟合参数向量$\beta$ ,使得
$$
J(\beta)=\left |X\beta-Y \right |^2_2-\left |k\beta \right |_1
$$
达到最小值,$\left |k\beta \right |_1$为目标函数的惩罚项,k为惩罚系数
lasson回归
由于拟合Lasso回归模型参数时,使用的损失函数(机器学习中的用语)中包含惩罚系数k,因此在计算模型回归系数之前,仍然需要得到最理想的k值,与岭回归模型类似,k值的确定可以通过定性的可视化方法.
例题
用此方法求解:(上面题的Lasso回归的题目)
Malinvand于1966年提出的研究法国经济问题的一组数据,如下表1. 所考虑的因变量为进口总额y , 三个解释变量分别为:国内总产值x1、储存量x2、总消费x3(单位均为10亿法郎). 建立y与x1、x2、x3的关系
| 年份 | $x_1$ | $x_2$ | $x_3$ | $y$ | 年份 | $x_1$ | $x_2$ | $x_3$ | $y$ |
|---|---|---|---|---|---|---|---|---|---|
| 1949 | 149.3 | 4.2 | 108.1 | 15.9 | 1955 | 202.1 | 2.1 | 146.0 | 22.7 |
| 1950 | 171.5 | 4.1 | 114.8 | 16.4 | 1956 | 212.4 | 5.6 | 154.1 | 26.5 |
| 1951 | 175.5 | 3.1 | 123.2 | 19.0 | 1957 | 226.1 | 5.0 | 162.3 | 28.1 |
| 1952 | 180.8 | 3.1 | 126.9 | 19.1 | 1958 | 231.9 | 5.1 | 164.3 | 27.6 |
| 1953 | 190.7 | 1.1 | 132.1 | 18.8 | 1959 | 239.0 | 0.7 | 167.6 | 26.3 |
| 1954 | 202.1 | 2.2 | 137.7 | 20.4 |
1 | import numpy as np |
例题
在建立中国私人轿车拥有量模型时,主要考虑一下因素:
- 城镇居民家庭人均可支配收入$x_1$元
- 全国城镇人口$x_2$亿元
- 全国汽车产量$x_3$万辆
- 全国公路长度$x_4$万千米
- 中国私人轿车拥有量为 $y$ 万辆
求建立y的经验公式
| 年份 | $x_1$ | $x_2$ | $x_3$ | $x_4$ | $y$ |
|---|---|---|---|---|---|
| 1994 | 3496.2 | 3.43 | 136.69 | 111.78 | 205.42 |
| 1995 | 4283 | 3.52 | 145.27 | 115.7 | 249.96 |
| 1996 | 4838.9 | 3.73 | 147.52 | 118.58 | 289.67 |
| 1997 | 5160.3 | 3.94 | 158.25 | 122.64 | 358.36 |
| 1998 | 5425.1 | 4.16 | 163 | 127.85 | 423.65 |
| 1999 | 5854 | 4.37 | 183.2 | 135.17 | 533.88 |
| 2000 | 6280 | 4.59 | 207 | 140.27 | 625.33 |
| 2001 | 6859.6 | 4.81 | 234.17 | 169.8 | 770.78 |
| 2002 | 7702.8 | 5.02 | 325.1 | 176.52 | 968.98 |
解 ==(建模思路:可先用普通最小二乘法建立模型,找出不足,然后提出用Lasso模型进行改进,这样体现了建模的逐渐深入和完善的过程,论文也有层次)==
首先,最小二乘法建立y与变量之间的关系
1 | import numpy as np |
out:
1 | OLS Regression Results |
这里曲线拟合$R^2=0.999$ 拟合效果很好,但是看到$x_1系数<0$所以不符合现实,且在显著水平$\alpha=0.05$下,x1对y不显著。
这里输出结果中,写出了所有变量前面的系数。
$$
\hat{y}=-1028.4134-0.0159x_1+245.6120x_2+1.6316x_3+2.0294x_4
$$
所以我们要优化:Lasso回归部分
1 | import numpy as np |
拓展阅读:(了解就可以了,明白什么时候选择Lasso回归合适.)
对于高维数据,维数灾难所带来的过拟合问题,其解决思路是:1)增加样本量;2)减少样本特征,而对于现实情况,会存在所能获取到的样本数据量有限的情况,甚至远小于数据维度,即:d>>n。如证券市场交易数据、多媒体图形图像视频数据、航天航空采集数据、生物特征数据等。
主成分分析作为一种数据降维方法,其出发点是通过整合原本的单一变量来得到一组新的综合变量,综合变量所代表的意义丰富且变量间互不相关,综合变量包含了原变量大部分的信息,这些综合变量称为主成分。主成分分析是在保留所有原变量的基础上,通过原变量的线性组合得到主成分,选取少数主成分就可保留原变量的绝大部分信息,这样就可用这几个主成分来代替原变量,从而达到降维的目的。
主成分分析法只适用于数据空间维度小于样本量的情况,当数据空间维度很高时,将不再适用。
Lasso是另一种数据降维方法,该方法不仅适用于线性情况,也适用于非线性情况。Lasso是基于惩罚方法对样本数据进行变量选择,通过对原本的系数进行压缩,将原本很小的系数直接压缩至0,从而将这部分系数所对应的变量视为非显著性变量,将不显著的变量直接舍弃。
常用的数据清洗方法
在数据处理的过程中,一般都需要进行数据的清洗工作,如数据集是否存在重复、缺失,数据是否具有完整性和一致性、数据中是否存在异常值等. 当发现数据中存在如上可能的问题时,都需要有针对性地处理。现在介绍如何识别和处理重复观察、缺失值和异常值.
重复观测处理
运用pandas对读入的数据进行重复项检查,以及如何删除数据中的重复项。
| appcategory | appname | comments | install | love | size | update |
|---|---|---|---|---|---|---|
| 网上购物-商城-团购-优惠-快递 | 每日优鲜 | 1297 | 204.7万 | 89.00% | 15.16MB | 2017年10月11日 |
| 网上购物-商城 | 苏宁易购 | 577 | 7996.8万 | 73.00% | 58.9MB | 2017年09月21日 |
| 网上购物-商城-优惠 | 唯品会 | 2543 | 7090.1万 | 86.00% | 41.43MB | 2017年10月13日 |
| 网上购物-商城-优惠 | 唯品会 | 2543 | 7090.1万 | 86.00% | 41.43MB | 2017年10月13日 |
| 网上购物-商城 | 拼多多 | 1921 | 3841.9万 | 95.00% | 13.35MB | 2017年10月11日 |
| 网上购物-商城-优惠 | 寺库奢侈品 | 1964 | 175.4万 | 100.00% | 17.21MB | 2017年09月30日 |
| 网上购物-商城 | 淘宝 | 14244 | 4.6亿 | 68.00% | 73.78MB | 2017年10月13日 |
| 网上购物-商城-团购-优惠 | 当当 | 134 | 1615.3万 | 61.00% | 37.01MB | 2017年10月17日 |
| 网上购物-商城-团购-优惠 | 当当 | 134 | 1615.3万 | 61.00% | 37.01MB | 2017年10月17日 |
| 网上购物-商城-团购-优惠 | 当当 | 134 | 1615.3万 | 61.00% | 37.01MB | 2017年10月17日 |
这里很直观的看到有很多数据重复了。
方法:检查上述的数据集是否有重复,pandas中使用duplicated方法,该方法返回的是数据行每一行的检验结果,即每一行的返回一个bool值,使用drop_duplicates方法移除重复值。
1 | import pandas as pd |
缺失值处理
Pandas使用浮点值NaN表示浮点或浮点数组中的缺失数据,Python内置的None值也会被当作缺失值处理. Pandas使用方法isnull 检测是否为缺失值,检测对象的每个元素返回一个bool值.
1 | #检测是否有缺失值 |
三种方法
过滤法、删除法
- dropna方法,适用于缺失值的观测对象所占比例非常低(如5%以内),直接删除缺失值所在的观测对象。因为对结果影响不大
填充法、替换法
- 用某种常数值替换缺失值,使用fillna方法。例如对连续变量而言,用中位数或均值;对于离散变量,使用众数替换。
插值法
- 根据其他非缺失的变量或观测来预测缺失值,常见有线性插值法、K近邻插值法、Lagrange插值法等
对Excel文件数据进行数据(删除)过滤
1 | from pandas import read_excel |
对excel表中的确实值进行数据填充
1 | from pandas import read_excel |
数值型缺失数据利用插值法进行替换
1 | from pandas import read_excel |
异常值处理
异常值的检测一般采用两种方法:标准差法、箱线图法
太阳黑子个数文件sunspots.csv数据用Excel软件打开后的格式如C:\Users\墨羽辰\Documents\QQ\暑假打卡20_例6_sunspots.csv,共有289条记录,识别并处理其中的异常值。
1 | from pandas import read_csv |
线性规划
如何利用现有资源来安排生产,以取得最大经济效益的问题。
例 1 某机床厂生产甲、 乙两种机床, 每台销售后的利润分别为 4000 元与 3000 元。生产甲机床需用 A、 B 机器加工,加工时间分别为每台 2 小时和 1 小时;生产乙机床需用 A、 B、 C 三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为 A 机器 10 小时、 B 机器 8 小时和C 机器 7 小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
数学模型
| A | B | C | ||
|---|---|---|---|---|
| 4000 | 甲 | 2 | 1 | |
| 3000 | 乙 | 1 | 1 | 1 |
| 10 | 8 | 7 |
设甲机床有x1个,乙机床有x2个 (0)x1, x2 称之为决策变量
目标函数 max z = 4 x1 + 3x2 (1)目标函数
约束条件: (2)约束条件
2 x1 + x2 ≤ 10
x1 + x2 ≤ 8
x2 ≤ 7
x1,x2 ≥ 0
Matlab 中规定线性规划的标准形式为
$$
\min_{x} c^T x
$$
$$
s.t.\begin{cases} Ax\le b \ Aeq \cdot x = beq \lb \le x\le ub\end{cases}
$$
其中 c 和 x 为 n 维列向量, A 、 Aeq 为适当维数的矩阵, b 、 beq 为适当维数的列向量。
线性规划中
$$
\min_{x} c^T x \qquad s.t. \quad Ax \le b
$$
的Matlab标准型为
$$
\min_{x} -c^T x \qquad s.t. \quad -Ax \le -b
$$
可行解:满足目标 s.t. 最优解:满足可行解的情况下,更加接近目标函数 可行域:满足所用的可行解
注:跟高中所学的线性规划的题目相似。平移z函数
(2,6)点处,可能为非空点(无最优解),或者是实数点(有最优解)。
特别解释及定义:
多维空间中:R不再是二维平面了。我们成多维空间形成的可行域为多胞形。二维平面中最优点一般是顶点,多胞体我们称最优点为一下概念:
**定义一:称 n 维空间中的区域 R 为一凸集,若 ∀x1, x2 ∈ R 及 ∀λ ∈(0,1) ,有 λx1 + (1- λ)x2 ∈R **
**定义二: 设 R 为 n 维空间中的一个凸集, R 中的点 x 被称为 R 的一个极点,若不存在 x1、 x2 ∈ R 及λ ∈(0,1) ,使得 x = λx1 + (1- λ)x2 **
解释:
[1]. 定义1 说明凸集中任意两点的连线必在此凸集中;
[2]. 定义 2 说明,若 x 是凸集 R的一个极点,则 x 不能位于 R 中任意两点的连线上。
一:单纯形法 —遍历法
一般线性规划问题中当线性方程组的变量数大于方程个数,这时会有不定数量的解,而单纯形法是求解线性规划问题的通用方法。
具体步骤,从线性方程组找出一个个的单纯形,每一个单纯形可以求得一组解,然后再判断该解使目标函数值是增大还是变小了,决定下一步选择的单纯形。通过优化迭代,直到目标函数实现最大或最小值。
等我稍加学习后,在拿出来更新分享。
二:Matlab解法
重点:
Matlab 中规定线性规划的标准形式为
$$
\min_{x} c^T x
$$
$$
s.t.\begin{cases} Ax\le b \ Aeq \cdot x = beq \lb \le x\le ub\end{cases}
$$
其中 c 和 x 为 n 维列向量, A 、 Aeq 为适当维数的矩阵, b 、 beq 为适当维数的列向量。
**[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS) **
LB 和 UB 分别是变量 x 的下界和上界 x0 是 x 的初始值 OPTIONS 是控制参数
c 和 x 为 n 维列向量 A 、 Aeq 为适当维数的矩阵 b 、 beq 为适当维数的列向量。
$$
\min_{z} = 2x_1+3x_2-5x_3
\s.t.\begin{cases}
x_1+x_2+x_3=7\2x_1-5x_2+x_3 \ge 12 \x_1,x_2,x_3 \ge 0
\end{cases}
$$
Matlab编写:
1 | c = [2;3;-5]; |
三、python求解
scipy.optimize模块求解
scipy.optimize提供了一个线性求解线性规划的函数linprog
scipy中线性规划的标准形为:
$$
\min_{x}z= c^T x \
s.t.\begin{cases} Ax\le b, \
Aeq \cdot x = beq, \
Lb \le x\le Ub\end{cases}
$$
lingrop的基本调用格式为:
1 | from scipy.optimize import linprog |
c 和 x 为 n 维列向量,c 对应目标函数的系数变量
A 为适当维数的矩阵, b为适当维数的列向量;A,b分别对应不等式约束的系数向量和常数项
Aeq 为适当维数的矩阵,beq 为适当维数的列向量;Aeq,beq分别对应等式约束的系数向量和常数项
例题
$$
\min_{x}z= -x_1+4x_2 \
s.t.
\begin{cases}
-3x_1+\ \ x_2\leqslant\ \ \ \ 6\
\ \ \ \ \ x_1+2x_2 \leqslant\ \ \ \ 4 \
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_2 \geqslant -3
\end{cases}
$$
1 | from scipy.optimize import linprog |
目标函数的最小值: -21.99999984082497
最优解: [ 9.99999989 -2.99999999]
所以最优解为$x_1=10,x_2=-3$,目标 函数的最优值为 -22.
$$
\min z= x_1-2x_2-3x_3 \
s.t.
\begin{cases}
-2x_1+x_2+\ \ x_3\leqslant \ \ \ 9\
-3x_1+x_2+2x_3 \geqslant \ \ \ 4 \
\ \ \ 4x_1-2x_2-x_3 = -6 \
x_1\geqslant -10, x_2\geqslant 0,x_3取值无约束
\end{cases}
$$
化成标准型:
$$
\min w= -x_1+2x_2+3x_3 \
s.t.
\begin{cases}
-2x_1+x_2+\ \ x_3\leqslant \ \ \ 9\
\ \ \ 3x_1-x_2-2x_3 \leqslant -4 \
\ \ \ 4x_1-2x_2-x_3 = -6 \
x_1\geqslant -10, x_2\geqslant 0,x_3取值无约束
\end{cases}
$$
也就是说将所有都化为$ax_1+bx_2\leqslant c$的形式。
1 | from scipy.optimize import linprog |
即所求问题的最优解为
目标函数的最小值: 0.4000000006525579
最优解: [-1.60000000e+00 8.29738643e-11 -4.00000000e-01]
(注意x2的解为8.29674988x10-11 ,写成解的时候保留一位小数就是0.0,即0)
例题:
加工一种食用油需要精炼若干种原料油并把它们混合起来、原料油的来源有两类共5种:植物油VEG1、植物油VEG2、非植物油OIL1、非植物油OIL2、非植物油OIL3. 购买每种原料油的价格(英镑/吨)如下表1,最终产品以150英镑/吨的价格出售. 植物油和非植物油需要在不同的生成线上进行精炼. 每月能够精炼的植物油不超过200吨,非植物油不超过250吨;在精炼过程中,重量没有损失,精炼费用可忽略不计. 最终产品要符合硬度的技术条件. 按照硬度计量单位,它必须为3~6. 假定硬度的混合是线性的,而原材料的硬度如表2所示.
求:为使利润最大,应该怎样指定它的月采购和加工计划
| 原料油 | VEG1 | VEG2 | OIL1 | OIL2 | OIL3 |
|---|---|---|---|---|---|
| 价格 | 110 | 120 | 130 | 110 | 115 |
| 原料油 | VEG1 | VEG2 | OIL1 | OIL2 | OIL3 |
|---|---|---|---|---|---|
| 硬度值 | 8.8 | 6.1 | 2.0 | 4.2 | 5.0 |
解:设$x_1,x_2,…,x_5$分别对应了5种原料油吨数,$x_6$为每月加工的成品油吨数
目标函数是要让净利润达到最大:即
$$
z=-100x_1-120x_2-130x_3-110x_4-115x_5+150x_6
$$约束条件为以下四类:
i.精炼能力的限制
植物油精炼能力的限制:$x_1+x_2\leqslant 200$
非植物油精炼能力的限制:$x_3+x_4+x_5\leqslant 250$
ii.硬度的限制
硬度上限:$8.8x_1+6.1x_1+2.0x_3+4.2x_4+5.0x_5\leqslant 6x_6$
硬度下限:$8.8x_1+6.1x_1+2.0x_3+4.2x_4+5.0x_5\geqslant3x_6$
iii.守恒性质限制(重量没有损失)
$x_1+x_1+x_3+x_4+x_5=x_6$
iiii.非负性限制
$x_i\geqslant0,i=0,1,…,6$
所以建立如下的线性规划
$$
max\ z=-100x_1-120x_2-130x_3-110x_4-115x_5+150x_6\
s.t.
\begin{cases}
x_1+x_2\leqslant 200\
x_3+x_4+x_5\leqslant 250\
8.8x_1+6.1x_1+2.0x_3+4.2x_4+5.0x_5\leqslant 6x_6\
8.8x_1+6.1x_1+2.0x_3+4.2x_4+5.0x_5\geqslant3x_6\
x_1+x_1+x_3+x_4+x_5=x_6\
x_i\geqslant0,i=0,1,…,6 .
\end{cases}
$$
要先转变成标准型即:
$$
这种函数\
\min_{x}z= c^T x \
s.t.\begin{cases} Ax\le b, \
Aeq \cdot x = beq, \
Lb \le x\le Ub\end{cases}
$$
所以得到为:
$$
max\ z=-100x_1-120x_2-130x_3-110x_4-115x_5+150x_6\
s.t.
\begin{cases}
x_1+x_2\leqslant 200\
x_3+x_4+x_5\leqslant 250\
8.8x_1+6.1x_1+2.0x_3+4.2x_4+5.0x_5-6x_6\leqslant 0\
-8.8x_1-6.1x_1-2.0x_3-4.2x_4-5.0x_5+3x_6\leqslant0\
x_1+x_1+x_3+x_4+x_5-x_6=0\
x_i\geqslant0,i=0,1,…,6 .
\end{cases}
$$
程序:
1 | from scipy.optimize import linprog |
目标函数的最小值: -4.1769028848418895e-13
最优解为: [1.16766018e-16 2.24124639e-15 3.48701448e-16 1.33739624e-15
2.13371900e-15 2.00505560e-15]
已知某种商品6个仓库的存活量,8个客户对该商品的需求量,单位商品运价如下表3所示. 试确定6个仓库到8个客户的商品调运数量,使总的运输费用最小.
| 仓库W|单价运价右下\客户V | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | 存货量 |
|---|---|---|---|---|---|---|---|---|---|
| $W_1$ | 6 | 2 | 6 | 7 | 4 | 2 | 5 | 9 | 60 |
| $W_2$ | 4 | 9 | 5 | 3 | 8 | 5 | 8 | 2 | 55 |
| $W_3$ | 5 | 2 | 1 | 9 | 7 | 4 | 3 | 3 | 51 |
| $W_4$ | 7 | 6 | 7 | 3 | 9 | 2 | 7 | 1 | 43 |
| $W_5$ | 2 | 3 | 9 | 5 | 7 | 2 | 6 | 5 | 41 |
| $W_6$ | 5 | 5 | 2 | 2 | 8 | 1 | 4 | 3 | 52 |
| 需求量 | 35 | 37 | 22 | 32 | 41 | 32 | 43 | 38 |
解:设
$x_{ij}(i=1,2,…,6;j=1,2,…,8)$表示第i个仓库到第j个客户的商品数量,
$c_{ij}(i=1,2,…,6;j=1,2,…,8)$表示第i个仓库运到第j个客户的单位运价,
$d_{j}$表示第j个客户的需求量
$e_i$表示第i个仓库的库存量
建立线性规划模型:
$$
min \sum_{i=1}^{6}\sum_{j=1}^{8}c_{ij}x_{ij},\
s.t.
\begin{cases}
\sum_{j=1}^{8}x_{ij}\leqslant e_i,i=1,2,…,6\
\sum_{i=1}^{6}x_{ij}\leqslant d_j,j=1,2,…,6\
x_{ij}\geqslant0,i=1,2,…,6;j=1,2,…,8. \
\end{cases}
$$
1 | ''' |
灵敏度分析
灵敏度分析是指对系统因周围条件变化显示出来的敏感程度的分析.
在上一个例题中,都设定了$c_{ij},d_j,e_i$等为常数,但实际问题中,这些系数往往是估计值,或者预测值,经常有少许的变动。
所以提出几点问题
- 如果参数$c_{ij},d_j,e_i$中的一个或几个发生变化,现行最优方案会有什么变化?
- 将这些参数的变化限制在什么范围下,原最优解任然是最优解?
实际上,给定参数量一个步长使其重复求解线性规划问题,以观察最优解的变化情况,这是一个可用的数值方法,特别是计算机求解时。
例题
一家奶制品加工厂用牛奶生成A、B两种奶制品,1桶牛奶可以在甲类设备上用12 h加工成3kg A,或者在乙类设备上用8h 加工成4kg B. 假定根据市场需求,生成的A,B全部能售出,且每千克A 获利24元,每千克B 获利16 元. 现在加工厂每天能得到50 桶牛奶的供应,每天正式工人总的劳动时间为480 h,并且甲类设备每天至多能加工100kg A,乙类设备的加工能力没有限制. 试为该厂指定一个生产计划,使每天获利最大,并进一步讨论以下两个附加问题:
(1) 若可以聘用临时工人以增加劳动时间,是否聘用临时工人.
(2) 假设由于市场需求变化,每千克A 的获利增加到30元,是否改变生成计划.
解:设$x_1$桶牛奶生成A,$x_2$桶牛奶生成B,每天获利z元
建立方程有:
$$
min\ z=324x_1+416x_2=72x_1+64x_2\
s.t.
\begin{cases}
x_1+x_2\leqslant 50\
12x_1+8x_2\leqslant 480\
3x_1\leqslant 100\
x_1>0,x_2>0
\end{cases}
$$
求解
1 | ##我的 |
为什么c=[-72,-64]呢?
- 是因为本来这个函数求解的就是最小值,那么要求解最小值的话,变为负数就成为了最大值,但是符号相反。
所以最优解为:$x_1=20;x_2=30$,收益最大化为3360元。
松弛问题slack
- 经过求解可知(slack的两个分量都是0),两个约束条件都是“紧约束”,即最优解是不等式的约束条件达到了边界,约束条件此时实际上是等式约束,(1)所以增加劳动时间,会提高收益,因而附加问题(1)应该聘用临时工人.
问题二:
当每千克A 的获利增加到30元
$$
min\ z=330x_1+416x_2=90x_1+64x_2\
s.t.
\begin{cases}
x_1+x_2\leqslant 50\
12x_1+8x_2\leqslant 480\
3x_1\leqslant 100\
x_1>0,x_2>0
\end{cases}
$$
方程几乎不变,只是改变了最优函数。
1 | from scipy.optimize import linprog |
最优解不变,但是获得的价为3720.0。所以生产计划不变。
整数规划与非线性规划
整数规划
线性规划的变量是连续型的,但如果变量是离散的非负整数值才有意义,就是整数线性规划,简称整数规划(问题依旧不变,但是物品类似不可分,导致得到的解只有整数解)
求解下列整数线性规划问题
$$
min\ z=40x_1+90x_2\
s.t.
\begin{cases}
9x_1+7x_2\leqslant 56\
-7x_1+-20x_2\leqslant -70\
x_1>0,x_2>0且为整数
\end{cases}
$$
1 | import cvxpy as cp |
最优值为: 350.0 最优解为: [2. 3.]
指派问题及求解
标准指派模型
标准指派问题的数学模型表现为0-1整数规划的形式,当然可以通过整数规划的算法求最优解,但是标准指派问题的数学具有独特的结构,可采用著名的匈牙利算法求标准指派问题的最优解。
某商业公司计划开办5家新商店,决定由5家建筑公司分别承建. 已知建筑公司$A_i(i=1,..,5)$,对新商店$B_j(j=1,..,5)$的建造费用的报价(万元)为$c_{ij}(i,j=1,..,5)$,如下。为了节省费用,商业公司应当对5家建筑公司怎样分配建造任务,才能使总的建造费最少?
| $B_1$ | $B_2$ | $B_3$ | $B_4$ | $B_5$ | |
|---|---|---|---|---|---|
| $A_1$ | 4 | 8 | 7 | 15 | 12 |
| $A_2$ | 7 | 9 | 17 | 14 | 10 |
| $A_3$ | 6 | 9 | 12 | 8 | 7 |
| $A_4$ | 6 | 7 | 14 | 6 | 10 |
| $A_5$ | 6 | 9 | 12 | 10 | 6 |
解:这是一个标准的指派问题. 引进0-1变量
$$
x_{ij}
\begin{cases}
1,A_i承建B_j;\
0,A_i不承建B_j;\
\end{cases}
\ \ \ (i,j=1,2,3,4,5)
$$
建立数学模型:
$$
min\ z=\sum_{i=1}^{5}\sum_{j=1}^{5}c_{ij}+x_{ij}\
s.t.
\begin{cases}
\sum_{j=1}^{5}x_{ij}=1,i=1,2,…,5\
\sum_{i=1}^{5}x_{ij}=1,i=1,2,…,5\
x_{ij}=0\ or\ 1,(i,j=1,2,…,5)
\end{cases}
(意思是每个房子都要建且只能是一个建筑队去建且要不不建要不建)
$$
1 | import numpy as np |
广义指派模型
最大化指派模型
在实际应用中,常会遇到各种非标准形式的指派问题—广义指派问题,通常的处理方法是先讲它们转化为标准形式,然后再用匈牙利算法求解.
一些指派问题中,每人完成各项工作的效率可能是诸如利润、业绩等(效益型指标/指标体现),此时则以总的工作效率最大为目标函数,即
$$
max\ z=\sum_{i=1}^{n}\sum_{j=1}^{n}c_{ij}x_{ij}
$$
对于最大化指派问题,若令:
$$
M=\max_{i\leqslant n,j\leqslant n} {c_{ij} }
$$
再由于约束函数条件的限制
$$
\sum^{n}{i=1}\sum{j=1}^{n}x_{ij}=n
$$
则有:
$$
min\sum_{i=1}^{n}\sum_{j=1}^{n}(M-c_{ij})x_{ij}\
=min(\sum_{i=1}^{n}\sum_{j=1}^{n}Mx_{ij}-\sum_{i=1}^{n}\sum_{j=1}^{n}c_{ij}x_{ij})\
=nM-max\sum_{i=1}^{n}\sum_{j=1}^{n}c_{ij}x_{ij}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
$$
即
$$
max\sum_{i=1}^{n}\sum_{j=1}^{n}c_{ij}x_{ij}=
nM-min\sum_{i=1}^{n}\sum_{j=1}^{n}(M-c_{ij})x_{ij}
$$
于是,使得$C=(c_{ij}){n\times n}$为效率矩阵的最大化指派问题,就转化为求以$(M-c{ij})_{n\times n}$为效率矩阵的标准指派问题。
人数和任务数不等的指派问题
- 若人数少于任务数,添加虚拟的“人”,对应的效率取为0
- 若人数多于任务数,添加虚拟的“任务”,对应的效率取为0
一个人可完成多项任务的指派问题
- 可将该人看作相同的几个人来接受指派,只需令其完成同一项任务的效率都一样即可
某项任务一定不能由某人完成的指派问题
- 对于这样的指派问题,只需将相应的效率值取成足够大的数即可.
注意:上述是理论推导,在实际使用软件求解广义指派问题时,也可直接建立0-1整数规划模型,不需要把广义指派问题化成标准的指派问题.